
Fernando de Goes, Doug L. James
Abstract:
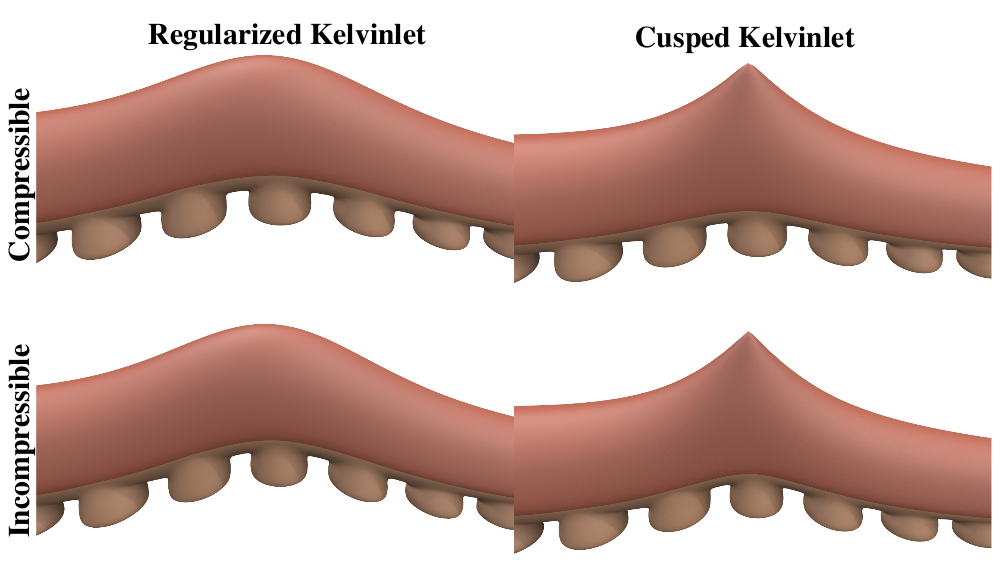
In this work, we present an extension of the regularized Kelvin-let technique suited to non-smooth, cusp-like edits. Our approach is based on a novel multi-scale convolution scheme that layers Kelvinlet deformations into a finite but spiky solution, thus offering physically based volume sculpting with sharp falloff profiles. We also show that the Laplacian operator provides a simple and effective way to achieve elastic displacements with fast far-field decay, thereby avoiding the need for multi-scale extrapolation. Finally, we combine the multi-scale convolution and Laplacian machinery to produce Sharp Kelvinlets, a new family of analytic fundamental solutions of linear elasticity with control over both the locality and the spikiness of the brush profile. Closed-form expressions and reference implementation are also provided.
Paper (PDF)
Additional materials: [code.zip]
Video

