Charles Loop, Tony D. DeRose
Abstract:
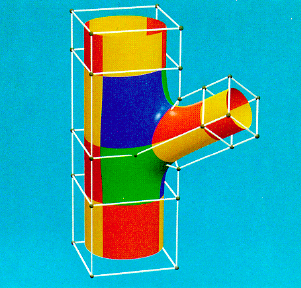
B-spline surfaces, although widely used, are incapable of describing surfaces of arbitrary topology. It is not possible to model a general closed surface or a surface with handles as a single non-degenerate B-spline. In practice such surfaces are often needed. In this paper, we present generalizations of biquadratic and bicubic B-spline surfaces that are capable of capturing surfaces of arbitrary topology (although restrictions are placed on the connectivity of the control mesh). These results are obtained by relaxing the sufficient but not necessary smoothness constraints imposed by B-splines and through the use of an n-sided generalization of
Bezier surfaces called S-patches.
Available in the Proceedings of SIGGRAPH 1990.