 |
 |
Generalized B-splines for surfaces of arbitrary topology Charles Loop, Tony D. DeRose August 1990 B-spline surfaces, although widely used, are incapable of describing surfaces of arbitrary topology. It is not possible to model a general closed surface or a surface with handles as a single non-degenerate B-spline. In practice such surfaces are often needed. In this paper, we present generalizations of biquadratic and bicubic ... [more] Available in the Proceedings of SIGGRAPH 1990. |
 |
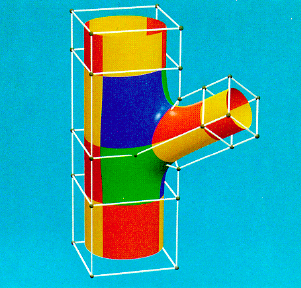
A Multisided Generalization of Bezier Surfaces Charles Loop, Tony D. DeRose July 1989 In this paper we introduce a class of surface patch representations, called S-patches, that unify and generalize triangular and tensor product Bezier surfaces by allowing patches to be defined over any convex polygonal domain; hence, S-patches may have any number of boundary curves. Other properties of S-patches are geometrically meaningful control points, separate control over ... [more] Available in Transactions on Graphics, Vol 8, No 3, July 1989. |