
 |
 |
Vector Field Processing on Triangle Meshes Fernando de Goes, Mathieu Desbrun, Yiying Tong August 2015 While scalar fields on surfaces have been staples of geometry processing, the use of tangent vector fields has steadily grown in geometry processing over the last two decades: they are crucial to encoding directions and sizing on surfaces as commonly required in tasks such as texture synthesis, non-photorealistic rendering, digital ... more Paper (PDF) SIGGRAPH Courses 2016, SIGGRAPH Asia Courses 2015 |
 |
Subdivision Exterior Calculus for Geometry Processing Fernando de Goes, Mathieu Desbrun, Mark Meyer, Tony DeRose April 2016 This paper introduces a new computational method to solve differential equations on subdivision surfaces. Our approach adapts the numerical framework of Discrete Exterior Calculus (DEC) from the polygonal to the subdivision setting by exploiting the refinability of subdivision basis functions. The resulting Subdivision Exterior Calculus (SEC) provides significant improvements in ... more Paper (PDF) Additional materials: [supplemental.pdf], [supplementalFigs.pdf] SIGGRAPH 2016 Available as Pixar Technical Memo #16-01 |
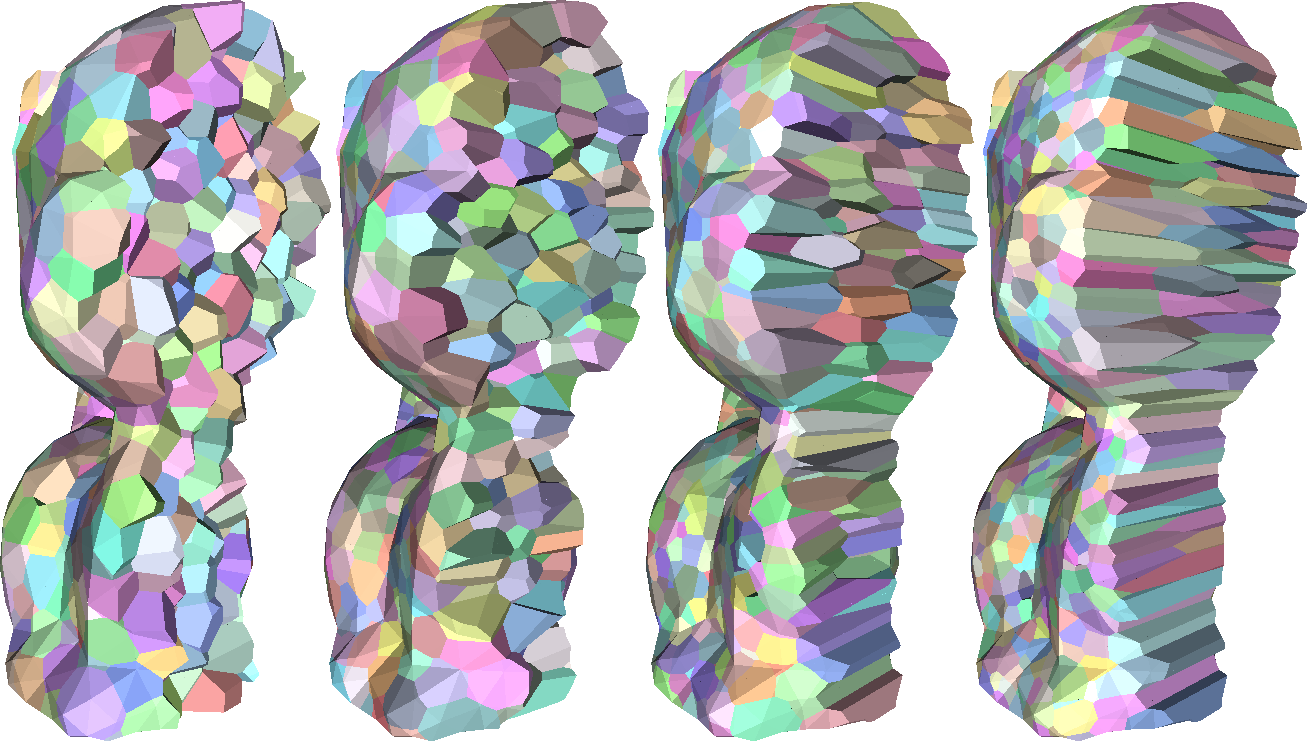 |
Optimal Voronoi Tessellations with Hessian-based Anisotropy Max Budninskiy, Beibei Liu, Fernando de Goes, Yiying Tong, Pierre Alliez, Mathieu Desbrun December 2016 This paper presents a variational method to generate cell complexes with local anisotropy conforming to the Hessian of any given convex function and for any given local mesh density. Our formulation builds upon approximation theory to offer an anisotropic extension of Centroidal Voronoi Tessellations which can be seen as a ... more Paper (PDF) Additional materials: [BLdG+16_SuppMat.pdf] SIGGRAPH Asia 2016 |
 |
Discrete Differential Operators on Polygonal Meshes Fernando de Goes, Andrew Butts, Mathieu Desbrun April 2020 Geometry processing of surface meshes relies heavily on the discretization of differential operators such as gradient, Laplacian, and covariant derivative. While a variety of discrete operators over triangulated meshes have been developed and used for decades, a similar construction over polygonal meshes remains far less explored despite the prevalence of ... more Paper (PDF) |
 |
Stochastic Computation of Barycentric Coordinates Fernando de Goes, Mathieu Desbrun April 2024 This paper presents a practical and general approach for computing barycentric coordinates through stochastic sampling. Our key insight is a reformulation of the kernel integral defining barycentric coordinates into a weighted least-squares minimization that enables Monte Carlo integration without sacrificing linear precision. Our method can thus compute barycentric coordinates directly ... more Paper (PDF) SIGGRAPH 2024 |