HBR Overview
Hierarchical Boundary Representation (Hbr)
Hbr is an interconnected topological data representation. The high level of vertex connectivity information makes this representation well suited for creation and editing purposes. It is however inefficient for interactive refinement operations: Separate objects are allocated for each vertex and edge with pointers to neighboring vertices and edges.
Hbr is also the lowest-level subdivision library in Pixar's Photorealistic RenderMan.
Note
As of OpenSubdiv 3.0, all Hbr dependencies have been removed from the core APIs (Sdc, Vtr, Far, Osd). The legacy source code of Hbr is provided purely for regression and legacy purposes. If your code is currently depending on Hbr functionality, we recommend migrating to the newer APIs as we cannot guarantee that this code will be maintained in future releases. For more information see the 3.0 release notes
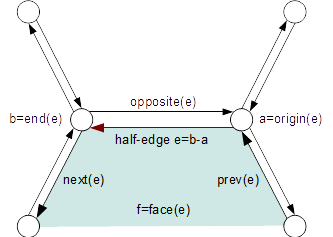
Half-edge Data Structure
The current implementation is based on a half-edge data structure.
Half-edge cycles and Manifold Topology
Because half-edges only carry a reference to their opposite half-edge, a given edge can only access a single neighboring edge cycle.
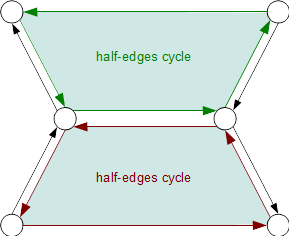
This is a fundamental limitation of the half-edge data structure, in that it cannot represent non-manifold geometry, in particular fan-type topologies. A different approach to topology will probably be necessary in order to accommodate non-manifold geometry.
Templated Vertex Class
The vertex class has been abstracted into a set of templated function accesses. Providing Hbr with a template vertex class that does not implement these functions allows client-code to use Hbr as a pure topological analysis tool without having to pay any costs for data interpolation. It also allows client-code to remain in complete control of the layout of the vertex data : interleaved or non-interleaved.
Boundary Interpolation Rules
Hbr recognizes 4 rule-sets of boundary interpolation:
| Interpolation Rule-Sets |
|---|
| k_InterpolateBoundaryNone |
| k_InterpolateBoundaryEdgeOnly |
| k_InterpolateBoundaryEdgeAndCorner |
| k_InterpolateBoundaryAlwaysSharp |
This enum is shared for both vertex and face-varying interpolation, with the following distinctions:
- vertex boundaries:
- the BoundaryNone rule skips all boundary vertices (results are ''undefined'')
- the AlwaysSharp rule does not apply
- face-varying boundaries:
- the BoundaryNone rule selects bilinear face-varying interpolation
