Use Fewer Spans

While polygon models need to use a large number of spans to approximate smooth curved surfaces, subdivision models require significantly fewer control points.

In most situations, 6 spans are enough to create accurate circular shapes, and 4 is often enough to approximate background objects.

Avoid High Valence vertices

A high valence vertex is a vertex connected to more than 4 adjacent edges.

High valence vertices cause several problems when subdivided:

• The Catmull-Clark scheme can produce "wavy" surfaces when a revolution vertex is surrounded by triangles (see here):

  

• High valence vertices incur fairly large performance hits

• Currently, OpenSubdiv has a hard constraint imposed by GPU shaders on the maximum valence of a vertex (~27 on current hardware)

Instead, here are some topological strategies to cap revolution shapes:

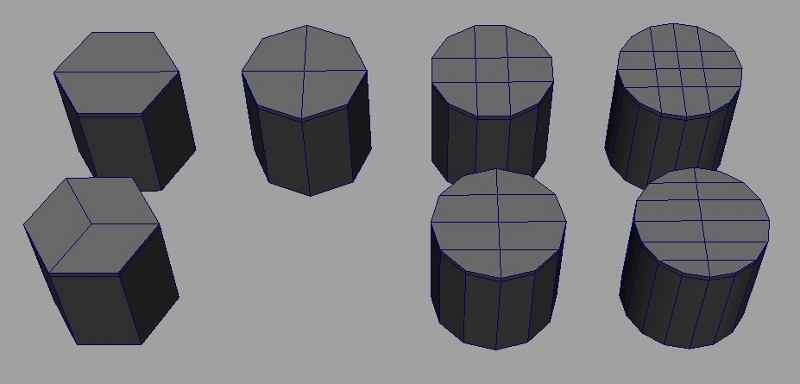
Note that all these cylinders use only quad faces, and all the vertices in the caps have a valence of 4 (except the bottom left example)

Edge-Loop Transitions

It is often necessary to vary the density of control vertices over the surface mesh: areas around the fingers of a hand require more CVs than the comparatively simpler region around the palm. It is important to handle the topology around these transitions efficiently.

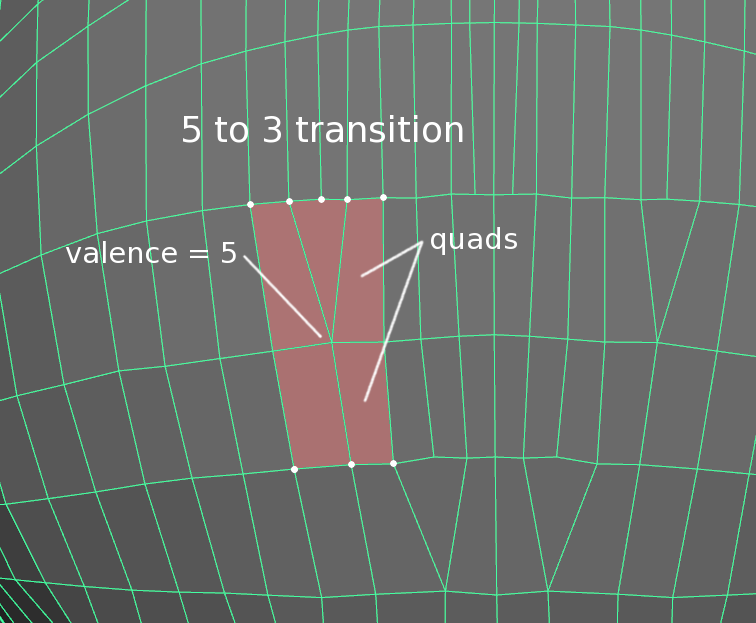
One strategy is to use extraordinary vertices, such as this example, using a valence 5 vertex to expand 3 edge loops into 5.

Practical Topology Primer

Some real-world examples showing how to produce detailed shapes with sparse topology, few extraordinary vertices, and no high-valence revolution poles.

Triangles and N-Gons

Used sparsely, non-quads can be very useful to gather 3 or more diverging edge-loops. These are often encountered in highly deforming areas with curvature saddle-points (ex: arm-torso connection). The strategic placement of a pentagon in one of these critical spots ensures that the surface remains smooth, while allowing for complex topology to flow around.

Use crease sets

Complex hard-surface models (giant robots, vehicles, buildings...) are likely to tag large number of edges : it is extremely useful to organize these edges/edge loops into logical sets with descriptive names. Edges or vertices in a crease set group all share the same sharpness value.

If you are modeling with Maya, the CreaseSetEditor implements this type of workflow. Additionally, for debugging purposes, it is often very helpful if the name of a set contains the sharpness value (ex: topDeck_2).

Besides authoring convenience, one of the benefits of having many edge-loops share identical sharpness values is that it enables very powerful performance optimizations within the feature adaptive algorithm (faster renders & less memory).