 |
 |
Toolglass and magic lenses: the see-through interface Eric A. Bier, Maureen Stone, Ken Pier, William Buxton, Tony D. DeRose August 1993 Toolglass widgets are new user interface tools that can appear, as though on a transparent sheet of glass, between an application and a traditional cursor. They can be positioned with one hand while the other positions the cursor. The widgets provide a rich and concise vocabulary for operating on application objects. These widgets may incorporate ... [more] Available in the Proceedings of SIGGRAPH 1993. |
 |
Interactive multiresolution surface viewing Andrew Certain, Jovan Popovic, Tony D. DeRose, Tom Duchamp, David H. Salesin, Werner Stuetzle August 1996 Not available. Available in the Proceedings of SIGGRAPH 1996. |
 |
Global illumination of glossy environments using wavelets and importance Per H. Christensen, Eric J. Stollnitz, David H. Salesin, Tony D. DeRose January 1996 We show how importance-driven refinement and a wavelet basis can be combined to provide an efficient solution to the global illumination problem with glossy and diffuse reflections. Importance is used to focus the computation on the interactions having the greatest impact on the visible solution. Wavelets are used to provide ... [more] Available in Transaction on Graphics, Vol 15, No 1, January 1996. |
 |
Wavelet Noise Robert L. Cook, Tony D. DeRose August 2005 Noise functions are an essential building block for writing procedural shaders in 3D computer graphics. The original noise function introduced by Ken Perlin is still the most popular because it is simple and fast, and many spectacular images have been made ... [more] Additional materials: [RapLyrics.txt] Available in the Proceedings of SIGGRAPH 2005 |
 |
Harmonic Coordinates Tony D. DeRose, Mark Meyer January 2006 Generalizations of barycentric coordinates in two and higher dimensions have been shown to have a number of applications in recent years, including finite element analysis, the definition of S-patches (n-sided generalizations of Bezier surfaces), free-form deformations, mesh parametrization, and interpolation. In this paper we present a new form of d ... [more] Additional materials: [movie.mp4] Available as Pixar Technical Memo #06-02 |
 |
Subdivision Surfaces in Character Animation Tony D. DeRose, Michael Kass, Tien Truong August 1998 The creation of believable and endearing characters in computer graphics presents a number of technical challenges, including the modeling, animation and rendering of complex shapes such as heads, hands, and clothing. Traditionally, these shapes have been modeled ... [more] Available in the Proceedings of SIGGRAPH 1998. |
 |
Functional composition algorithms via blossoming Tony D. DeRose, Ronald N. Goldman, Hans Hagen, Stephen Mann April 1993 In view of the fundamental role that functional composition plays in mathematics, it is not surprising that a variety of problems in geometric modeling can be viewed as instances of the following composition problem: given representations for two functions F and G, compute a representation of the function H = F o G. We ... [more] Available in Transactions on Graphics, Vol 12, No 2, April 1993. |
 |
Three-Dimensional Computer Graphics: A Coordinate-Free Approach Tony D. DeRose October 1992 This manuscript is intended as a rigorous introduction to the field of computer graphics at a level appropriate for advanced undergraduates and beginning graduate students in computer science. The intent is not to present a completely comprehensive survey of the field. Rather, the goal is to provide a firm, modern account of those topics within ... [more] Additional materials: [geometryC.tar], [thumbNail.tiff] |
 |
Composing Bezier Simplices Tony D. DeRose July 1988 This paper describes two algorithms for solving the following general problem: Given two polynomial maps f: Rn to RN and S: RN to Rd in Bezier simmplex form, find the composition map Stilde = S o f in Bezier simplex form... Available in Transactions on Graphics, Vol 7, No 3, July 1988. |
 |
Geometric continuity, shape parameters, and geometric constructions for Catmull-Rom splines Tony D. DeRose, Brian A. Barsky January 1988 Catmull-Rom splines have local control, can be either approximating or interpolating, and are efficiently computable. Experience with Beta-splines has shown that it is useful to endow a spline with shape parameters, used to modify the shape of the curve or surface independently of the defining control vertices. Thus it is ... [more] Available in Transactions on Graphics, Vol 7, No 1, January 1988. |
 |
Multiresolution Analysis of Arbitrary Meshes Matthias Eck, Tony D. DeRose, Tom Duchamp, Hugues Hoppe, Michael Lounsbery, Werner Stuetzle August 1995 In computer graphics and geometric modeling, shapes are often represented by triangular meshes. With the advent of laser scanning systems, meshes of extreme complexity are rapidly becoming commonplace. Such meshes are notoriously expensive to store, transmit, render, and are awkward to edit. Multiresolution analysis offers a simple, unified, and theoretically sound approach to dealing with these ... [more] Available in the Proceedings of SIGGRAPH 1995. |
 |
Efficient, Fair Interpolation using Catmull-Clark Surfaces Mark Halstead, Michael Kass, Tony D. DeRose August 1993 We describe an efficient method for constructing a smooth surface that interpolates the vertices of a mesh of arbitrary topological type. Normal vectors can also be interpolated at an arbitrary subset of the vertices. The method improves on existing interpolation techniques in that it is fast, robust and general. Our approach is to compute a ... [more] Available in the Proceedings of SIGGRAPH 1993. |
 |
Piecewise Smooth Surface Reconstruction Hugues Hoppe, Tony D. DeRose, Tom Duchamp, Mark Halstead, Hubert Jin, John McDonald, Jean Schweitzer, Werner Stuetzle August 1994 We present a general method for automatic reconstruction of accurate, concise, piecewise smooth surface models from scattered range data. The method can be used in a variety of applications such as reverse engineering, and the automatic generation of CAD models from physical objects. Novel aspects of the method are its ability to model surfaces of ... [more] Available in the proceedings of Siggraph, 1994 |
 |
Surface Reconstruction from Unorganized Points Hugues Hoppe, Tony D. DeRose, Tom Duchamp, John McDonald, Werner Stuetzle July 1992 We describe and demonstrate an algorithm that takes as input an unorganized set of points x_1, ..., x_n on or near an unknown manifold M, and produces as output a simplicial surface that approximates M. Neither the topology, the presence of boundaries, nor the geometry of M are assumed to be known in advance ... [more] Available in Proceedings of SIGGRAPH 1992 |
 |
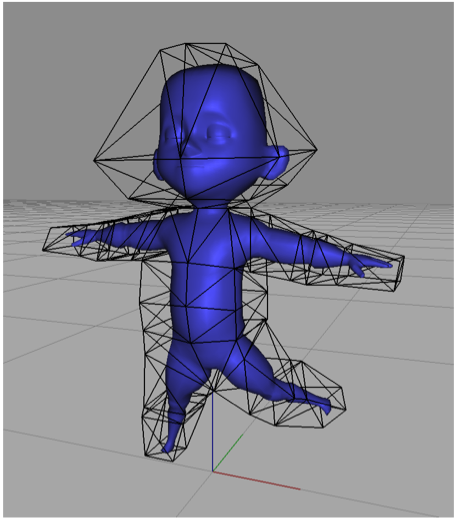
Harmonic Coordinates for Character Articulation Pushkar Joshi, Mark Meyer, Tony D. DeRose, Brian Green, Tom Sanocki August 2007 In this paper we consider the problem of creating and controlling volume deformations used to articulate characters for use in high-end applications such as computer generated feature films. We introduce a method we call harmonic coordinates that significantly improves upon existing volume deformation techniques. Our deformations are controlled using a topologically flexible structure, called a cage, ... [more] Available in Siggraph 2007. Available as Pixar Technical Memo #06-02b |
 |
Generalized B-splines for surfaces of arbitrary topology Charles Loop, Tony D. DeRose August 1990 B-spline surfaces, although widely used, are incapable of describing surfaces of arbitrary topology. It is not possible to model a general closed surface or a surface with handles as a single non-degenerate B-spline. In practice such surfaces are often needed. In this paper, we present generalizations of biquadratic and bicubic ... [more] Available in the Proceedings of SIGGRAPH 1990. |
 |
A Multisided Generalization of Bezier Surfaces Charles Loop, Tony D. DeRose July 1989 In this paper we introduce a class of surface patch representations, called S-patches, that unify and generalize triangular and tensor product Bezier surfaces by allowing patches to be defined over any convex polygonal domain; hence, S-patches may have any number of boundary curves. Other properties of S-patches are geometrically meaningful control points, separate control over ... [more] Available in Transactions on Graphics, Vol 8, No 3, July 1989. |
 |
Multiresolution Analysis for Surfaces of Arbitrary Topological Type Michael Lounsbery, Tony D. DeRose, Joe Warren January 1997 In this article, we present a new class of wavelets, based on subdivision surfaces, that radically extends the class of representable functions. Whereas previous two-dimensional methods were restricted to functions defined on R, the subdivision wavelets developed here may be applied to functions defined on compact surfaces of arbitrary topological type. ... [more] Available in ACM Transactions on Graphics, Vol. 16, No. 1, January 1997. |
 |
Computing Values and Derivatives of Bezier and B-spline Tensor Products Stephen Mann, Tony D. DeRose February 1995 We give an efficient algorithm for evaluating Bezier and B-spline tensor products for both positions and normals. The algorithm is an extension of a method for computing the position and tangent to a Bezier curve, and is asymptotically twice as fast as the standard bilinear algorithm. Available in CAGD, Vol 12, No. 1. |
 |
Hierarchical image caching for accelerated walkthroughs of complex environments Jonathan Shade, Dani Lischinski, David H. Salesin, Tony D. DeRose, John Snyder August 1996 Not available. Available in the Proceedings of SIGGRAPH 1996. |
 |
Wavelets for Computer Graphics: Theory and Applications Eric J. Stollnitz, Tony D. DeRose, David H. Salesin June 1996 From the Back Cover: This distinctly accessible introduction to wavelets provides computer graphics professionals and researchers with the mathematical foundations for understanding and applying this powerful tool.
Wavelets are rapidly becoming a core technique in computer graphics, with applications for: Image editing and compression; Automatic level-of-detail control for editing and rendering ... [more] |
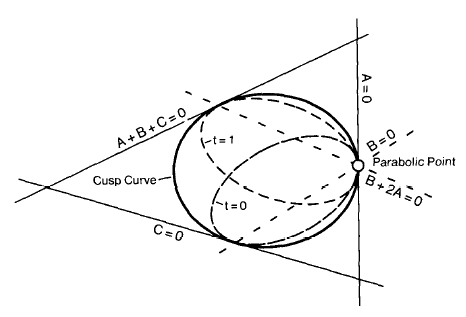 |
A geometric characterization of parametric cubic curves Maureen Stone, Tony D. DeRose July 1989 In this paper, we analyze planar parametric cubic curves to determine conditions for loops, cusps, or inflection points. By expressing the curve to be analyzed as a linear combination of control points, it can be transformed such that three of the control points are mapped to specific locations on the ... [more] Available in Transaction on Graphics, Vol 8, No 3, July 1989. |