|
 |
Convolutional Wasserstein Distances: Efficient Optimal Transportation on Geometric Domains Justin Solomon, Fernando de Goes, Gabriel Peyre, Marco Cuturi, Adrian Butscher, Andy Nguyen, Tao Du, Leonidas Guibas August 2015 This paper introduces a new class of algorithms for optimization problems involving optimal transportation over geometric domains. Our main contribution is to show that optimal transportation can be made tractable over large domains used in graphics, such as images and triangle meshes, improving performance by orders of magnitude compared to ... more Paper (PDF) SIGGRAPH 2015 |
 |
Vector Field Processing on Triangle Meshes Fernando de Goes, Mathieu Desbrun, Yiying Tong August 2015 While scalar fields on surfaces have been staples of geometry processing, the use of tangent vector fields has steadily grown in geometry processing over the last two decades: they are crucial to encoding directions and sizing on surfaces as commonly required in tasks such as texture synthesis, non-photorealistic rendering, digital ... more Paper (PDF) SIGGRAPH Courses 2016, SIGGRAPH Asia Courses 2015 |
 |
Subdivision Exterior Calculus for Geometry Processing Fernando de Goes, Mathieu Desbrun, Mark Meyer, Tony DeRose April 2016 This paper introduces a new computational method to solve differential equations on subdivision surfaces. Our approach adapts the numerical framework of Discrete Exterior Calculus (DEC) from the polygonal to the subdivision setting by exploiting the refinability of subdivision basis functions. The resulting Subdivision Exterior Calculus (SEC) provides significant improvements in ... more Paper (PDF) Additional materials: [supplemental.pdf], [supplementalFigs.pdf] SIGGRAPH 2016 Available as Pixar Technical Memo #16-01 |
 |
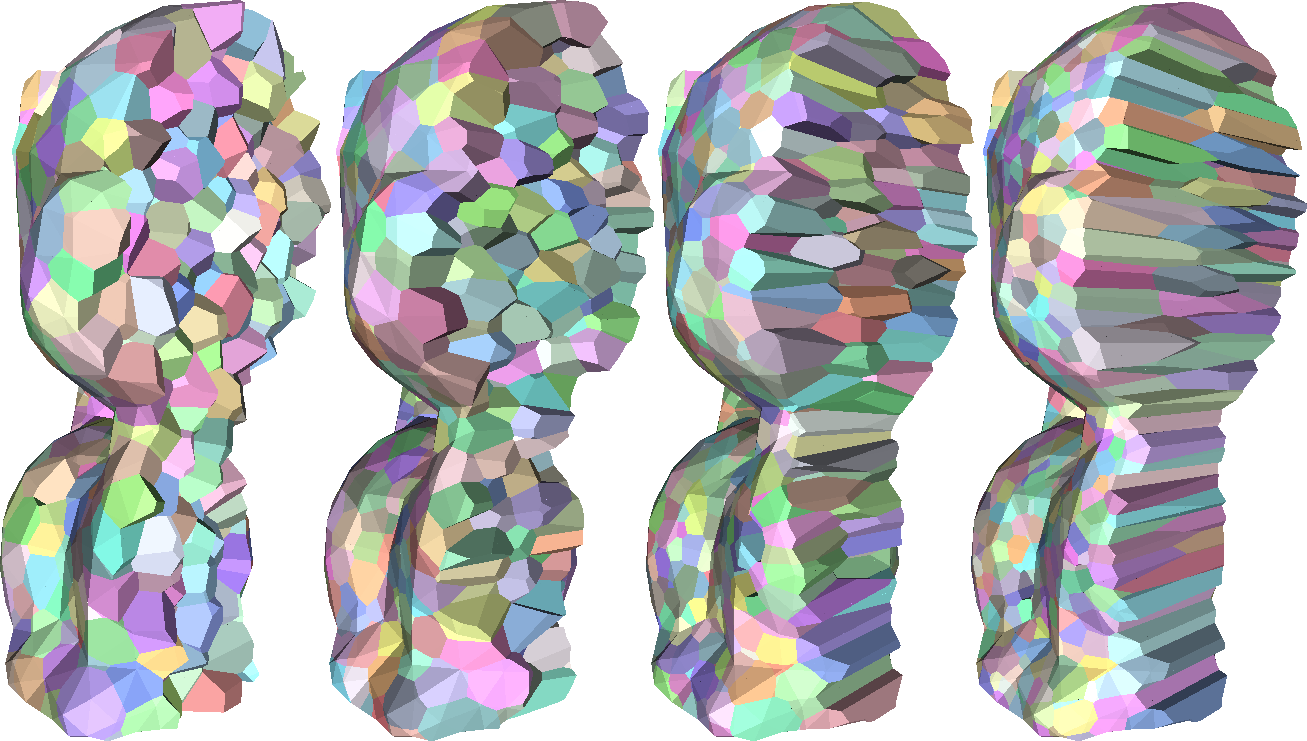Optimal Voronoi Tessellations with Hessian-based Anisotropy Max Budninskiy, Beibei Liu, Fernando de Goes, Yiying Tong, Pierre Alliez, Mathieu Desbrun December 2016 This paper presents a variational method to generate cell complexes with local anisotropy conforming to the Hessian of any given convex function and for any given local mesh density. Our formulation builds upon approximation theory to offer an anisotropic extension of Centroidal Voronoi Tessellations which can be seen as a ... more Paper (PDF) Additional materials: [BLdG+16_SuppMat.pdf] SIGGRAPH Asia 2016 |
 |
Regularized Kelvinlets: Sculpting Brushes based on Fundamental Solutions of Elasticity Fernando de Goes, Doug L. James May 2017 We introduce a new technique for real-time physically based volume sculpting of virtual elastic materials. Our formulation is based on the elastic response to localized force distributions associated with common modeling primitives such as grab, scale, twist, and pinch. The resulting brush-like displacements correspond to the regularization of fundamental solutions ... more Paper (PDF) Video: Regularized Kelvinlets Video: Additional example with ~2M triangles Additional materials: [gradDerivation.pdf], [multiScaleDerivation.pdf] SIGGRAPH 2017 Available as Pixar Technical Memo #17-03 |
 |
Stable Neo-Hookean Flesh Simulation Breannan Smith, Fernando de Goes, Theodore Kim December 2017 Non-linear hyperelastic energies play a key role in capturing the fleshy appearance of virtual characters. Real-world, volume-preserving biological tissues have Poisson's ratios near 1/2, but numerical simulation within this regime is notoriously challenging. In order to robustly capture these visual characteristics, we present a novel version of Neo-Hookean elasticity. Our ... more Paper (PDF) Video Additional materials: [snh_code.tar.bz2], [stable_neo_hookean_supplement.pdf] Errata: The expression for alpha on the last line of Page 4 contained a typo that we have fixed. |
 |
Dynamic Kelvinlets: Secondary Motions based on Fundamental Solutions of Elastodynamics Fernando de Goes, Doug L. James May 2018 We introduce Dynamic Kelvinlets, a new analytical technique for real-time physically based animation of virtual elastic materials. Our formulation is based on the dynamic response to time-varying force distributions applied to an infinite elastic medium. The resulting displacements provide the plausibility of volumetric elasticity, the dynamics of compressive and shear ... more Paper (PDF) Video Additional materials: [code.zip], [suppl.zip] Available as Pixar Technical Memo #18-05 |
 |
Automating the Handmade: Shading Thousands of Garments for Coco Byron Bashforth, Fernando de Goes, Jacob Kuenzel, Jake Merrell, Athena Xenakis August 2018 Coco presented a challenge for the garment shading team. Firstly, the scale of the movie is significant with both the human and skeleton worlds filled with primary, secondary, and background characters. Secondly, the garments speak to a specific culture and our shading needed to be very detailed to ... more Paper (PDF) |
 |
Patch-based Surface Relaxation Fernando de Goes, William Sheffler, Michael Comet, Alonso Martinez, Aimei Kutt August 2018 From rigging to post-simulation cleanups, surface relaxation is a widely used procedure in feature animation. Over the years, Pixar has experimented with several techniques for this task, mostly based on variants of Laplacian smoothing. Notably, none of existing approaches are suited to reproduce the patch layout of a baseline mesh. ... more Paper (PDF) |
 |
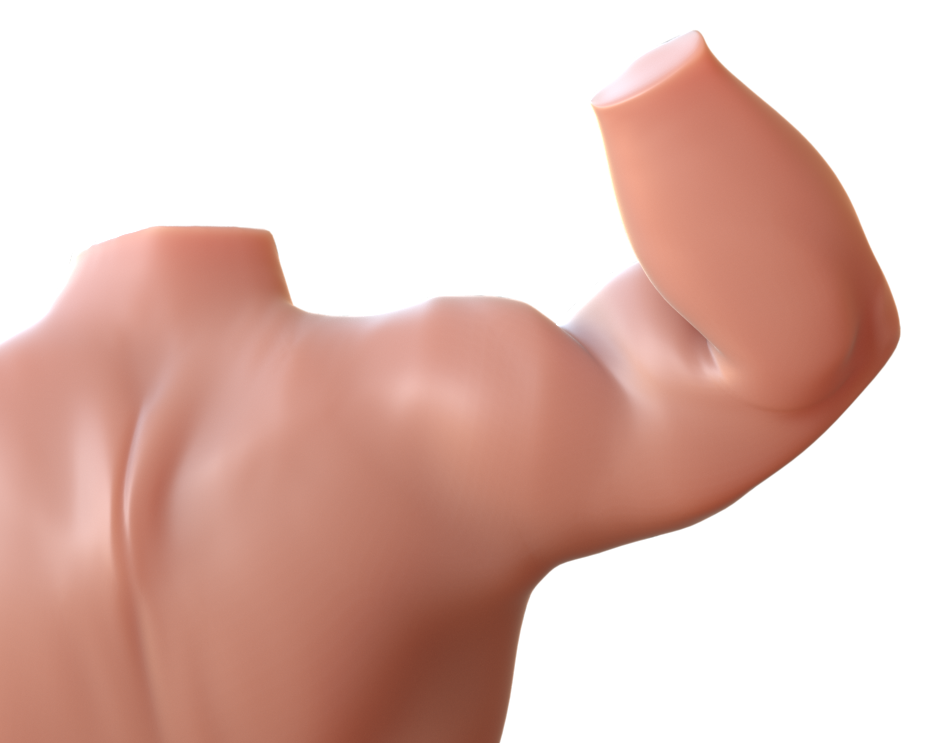
Analytic Eigensystems for Isotropic Distortion Energies Breannan Smith, Fernando de Goes, Theodore Kim September 2018 Many strategies exist for optimizing non-linear distortion energies in geometry and physics applications, but devising an approach that achieves the convergence promised by Newton-type methods remains challenging. In order to guarantee the positive semi-definiteness required by these methods, a numerical eigendecomposition or approximate regularization is usually needed. In this paper, ... more Paper (PDF) Additional materials: [Matlab.zip], [movie.mov], [supplement.pdf] |
 |
Anisotropic Elasticity for Inversion-Safety and Element Rehabilitation Theodore Kim, Fernando de Goes, Hayley Iben July 2019 We present an analysis of anisotropic hyperelasticity, specifically transverse isotropy, that obtains closed-form expressions for the eigendecompositions of many common energies. We then use these to build fast and concise Newton implementations. We leverage our analysis in two separate applications. First, we show that existing anisotropic energies are not inversion-safe, ... more Paper (PDF) Video Additional materials: [Anisotropy2019_supplement.pdf], [matlab.zip] |
 |
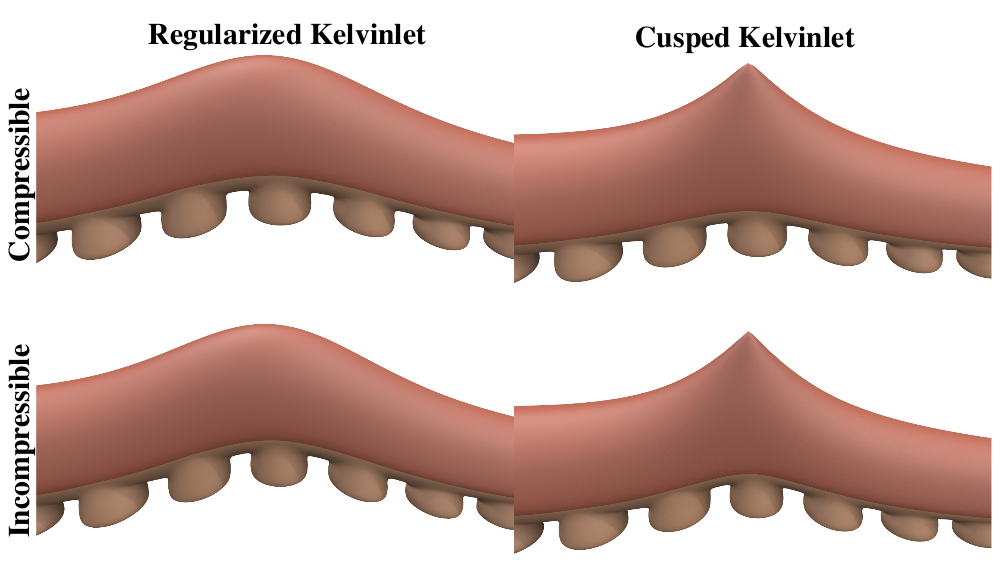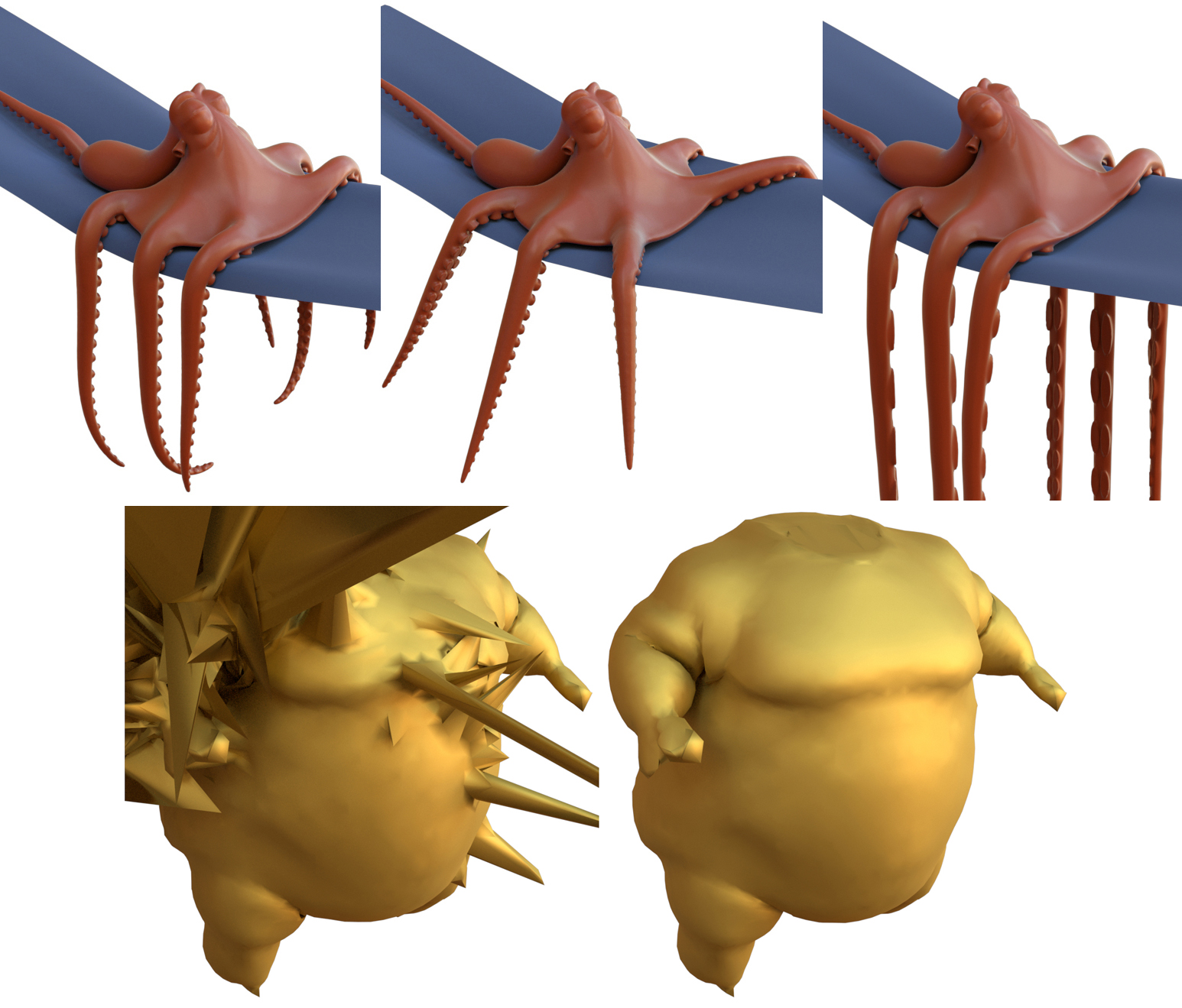
Sharp Kelvinlets: Elastic Deformations with Cusps and Localized Falloffs Fernando de Goes, Doug L. James July 2019 In this work, we present an extension of the regularized Kelvin-let technique suited to non-smooth, cusp-like edits. Our approach is based on a novel multi-scale convolution scheme that layers Kelvinlet deformations into a finite but spiky solution, thus offering physically based volume sculpting with sharp falloff profiles. We also show ... more Paper (PDF) Video Additional materials: [code.zip] |
 |
Discrete Differential Operators on Polygonal Meshes Fernando de Goes, Andrew Butts, Mathieu Desbrun April 2020 Geometry processing of surface meshes relies heavily on the discretization of differential operators such as gradient, Laplacian, and covariant derivative. While a variety of discrete operators over triangulated meshes have been developed and used for decades, a similar construction over polygonal meshes remains far less explored despite the prevalence of ... more Paper (PDF) |
 |
FaceBaker: Baking Character Facial Rigs with Machine Learning Sarah Radzihovsky, Fernando de Goes, Mark Meyer June 2020 Character rigs are procedural systems that deform a character's shape driven by a set of rig-control variables. Film quality character rigs are highly complex and therefore computationally expensive and slow to evaluate. We present a machine learning method for approximating facial mesh deformations which reduces rig computations, increases longevity of ... more Paper (PDF) Video |
 |
Garment Refitting for Digital Characters Fernando de Goes, Donald Fong, Meredith O'Malley June 2020 We present a new technique to refit garments between characters of different shapes. Our approach is based on a novel iterative scheme that alternates relaxation and rebinding optimizations. In the relaxation step, we use affine-invariant coordinates in order to adapt the input 3D garment to the shape of a target ... more Paper (PDF) Video |
 |
Sculpt Processing for Character Rigging Fernando de Goes, Patrick Coleman, Michael Comet, Alonso Martinez June 2020 Pose-space sculpting is a key component in character rigging workflows used by digital artists to create shape corrections that fire on top of deformation rigs. However, hand-crafting sculpts one pose at a time is notoriously laborious, involving multiple cleanup passes as well as repetitive manual edits. In this work, we ... more Paper (PDF) Video |
 |
Character Articulation through Profile Curves Fernando de Goes, William Sheffler, Kurt Fleischer 05 2022 Computer animation relies heavily on rigging setups that articulate character surfaces through a broad range of poses. Although many deformation strategies have been proposed over the years, constructing character rigs is still a cumbersome process that involves repetitive authoring of point weights and corrective sculpts with limited and indirect shaping ... more Paper (PDF) Video Video SIGGRAPH 2022 |
 |
Hair Emoting with Style Guides in Turning Red Brandon Montell, Fernando de Goes, Jacob Brooks May 2022 For Pixar's feature film Turning Red, the grooming and simulation teams faced the challenge of handling characters with millions of fur and hair curves, which often needed to behave differently in each shot reflecting the characters' emotional states. This work describes new tools developed to assist artists in managing and ... more Paper (PDF) Siggraph Talk 2022 |
 |
Revamping the Cloth Tailoring Pipeline at Pixar Christine Waggoner, Fernando de Goes May 2022 This work presents the most recent updates to the cloth tailoring pipeline at Pixar. We start by reviewing the evolution of cloth authoring tools used at Pixar from 2001 to the present day. Motivated by previous approaches, we introduce a structured workflow for cloth tailoring that manages multiple mesh versions ... more Paper (PDF) Siggraph Talk 2022 |
 |
A Procedural Approach for Stylized Bark Shading Alec Bartsch, Colin Thompson, Fernando de Goes May 2023 The Earth characters in Pixar's feature film Elemental (2023) called for a stylized look with bark patterns resembling organic locks of hair. To scale this custom shading to an entire class of background characters, we implemented an artistic-driven procedural workflow that offered rapid iterations on pattern generation without requiring extensive ... more Paper (PDF) SIGGRAPH Talks 2023 |
 |
Elemental Characters: Bringing Water to Life Max Gilbert, Jacob Kuenzel, Kris Campbell, Greg Gladstone, Jean-Claude Kalache, Fernando de Goes, Jon Barry May 2023 In Pixar's Elemental, the water characters of Element City are not drenched in water, but made of the element itself. Our goal was to create characters that felt non-human and of water, yet still maintain design, readability and charm. Starting with the concept art (inset) and at every step of ... more Paper (PDF) SIGGRAPH Talks 2023 |
 |
Shaping the Elements: Curvenet Animation Controls in Pixar's Elemental Duc Nguyen, Jeremie Talbot, William Sheffler, Mark Hessler, Kurt Fleischer, Fernando de Goes May 2023 We present a new shaping rig for authoring layers of animation control that facilitate surface editing in shot work. Our approach expands the curvenet rigging technology [de Goes et al. 2022] by introducing new tools that auto-generate a surface-aligned direct manipulator per curvenet knot. As a result, we obtain a ... more Paper (PDF) SIGGRAPH Talks 2023 |
 |
Stylizing Ribbons: Computing Surface Contours with Temporally Coherent Orientations Nora S Willett, Fernando de Goes, Kurt Fleischer, Mark Meyer, Chris Burrows September 2023 Line work is a core element for the stylization of computer animations used by recent shows. However, existing stylization tech- niques are limited to edge treatments based on brush strokes or textures applied solely on top of curves. In this work, we propose new stylization effects by offering artists direct ... more Paper (PDF) IEEE Transactions on Visualization and Computer Graphics |
 |
Stochastic Computation of Barycentric Coordinates Fernando de Goes, Mathieu Desbrun April 2024 This paper presents a practical and general approach for computing barycentric coordinates through stochastic sampling. Our key insight is a reformulation of the kernel integral defining barycentric coordinates into a weighted least-squares minimization that enables Monte Carlo integration without sacrificing linear precision. Our method can thus compute barycentric coordinates directly ... more Paper (PDF) SIGGRAPH 2024 |
 |
Wig Refitting in Pixar's Inside Out 2 Ben Porter, Jacob Speirs, Fernando de Goes May 2024 In Pixar's feature animation Inside Out 2 (2024), emotion characters are identified with their corresponding human characters by exhibiting similar wigs. To achieve this look, we developed a custom rig that assists the sharing and reuse of hair grooms between characters of different shapes, feature proportions, and mesh connectivities. Our ... more Paper (PDF) SIGGRAPH Talks 2024 |