Subdivision Surfaces
Overview
Subdivision surfaces are a common modeling primitive that has gained popularity in animation and visual effects over the past decades.



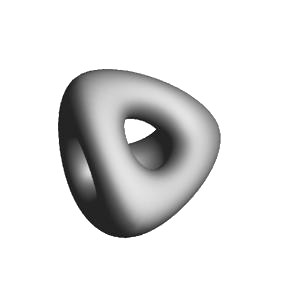
As the name suggests, subdivision surfaces are fundamentally surfaces.
More specifically, subdivision surfaces are piecewise parametric surfaces defined over meshes of arbitrary topology -- both concepts that will be described in the sections that follow.
Subdivision is both an operation that can be applied to a polygonal mesh to refine it, and a mathematical tool that defines the underlying smooth surface to which repeated subdivision of the mesh converges. Explicit subdivision is simple to apply some number of times to provide a smoother mesh, and that simplicity has historically lead to many tools representing the shape this way. In contrast, deriving the smooth surface that ultimately defines the shape -- its "limit surface" -- is considerably more complex but provides greater accuracy and flexibility. These differences have led to confusion in how some tools expose subdivision surfaces.
The ultimate goal is to have all tools use subdivision surfaces as true surface primitives. The focus here is therefore less on subdivision and more on the nature of the surface that results from it. In addition to providing a consistent implementation of subdivision -- one that includes a number of widely used feature extensions -- a significant value of OpenSubdiv is that it makes the limit surface more accessible.
Since its introduction, OpenSubdiv has received interest from users and developers with a wide variety of skills, interests and backgrounds. This document is intended to present subdivision surfaces from a perspective helpful in making use of OpenSubdiv. One purpose it serves is to provide a high level overview for those with less experience with the algorithms or mathematics of subdivision. The other is to provide an overview of the feature set available with OpenSubdiv, and to introduce those capabilities with the terminology used by OpenSubdiv (as much of it is overloaded).
Piecewise Parametric Surfaces
Piecewise parametric surfaces are arguably the most widely used geometric representation in industrial design, entertainment and many other areas. Many of the objects we deal with everyday -- cars, mobile phones, laptops -- were all designed and visualized first as piecewise parametric surfaces before those designs were approved and pursued.
Piecewise parametric surfaces are ultimately just collections of simpler modeling primitives referred to as patches. Patches constitute the "pieces" of the larger surface in much the same way as a face or polygon constitutes a piece of a polygonal mesh.
Parametric Patches
Patches are the building blocks of piecewise smooth surfaces, and many different kinds of patches have evolved to meet the needs of geometric modeling. Two of the more effective and common patches are illustrated below:
Single bicubic B-Spline patch |
Single bicubic Bezier patch |
Patches consist of a set of points or vertices that affect a rectangular piece of smooth surface (triangular patches also exist). That rectangle is "parameterized" in its two directions, transforming a simple 2D rectangle into the 3D surface:
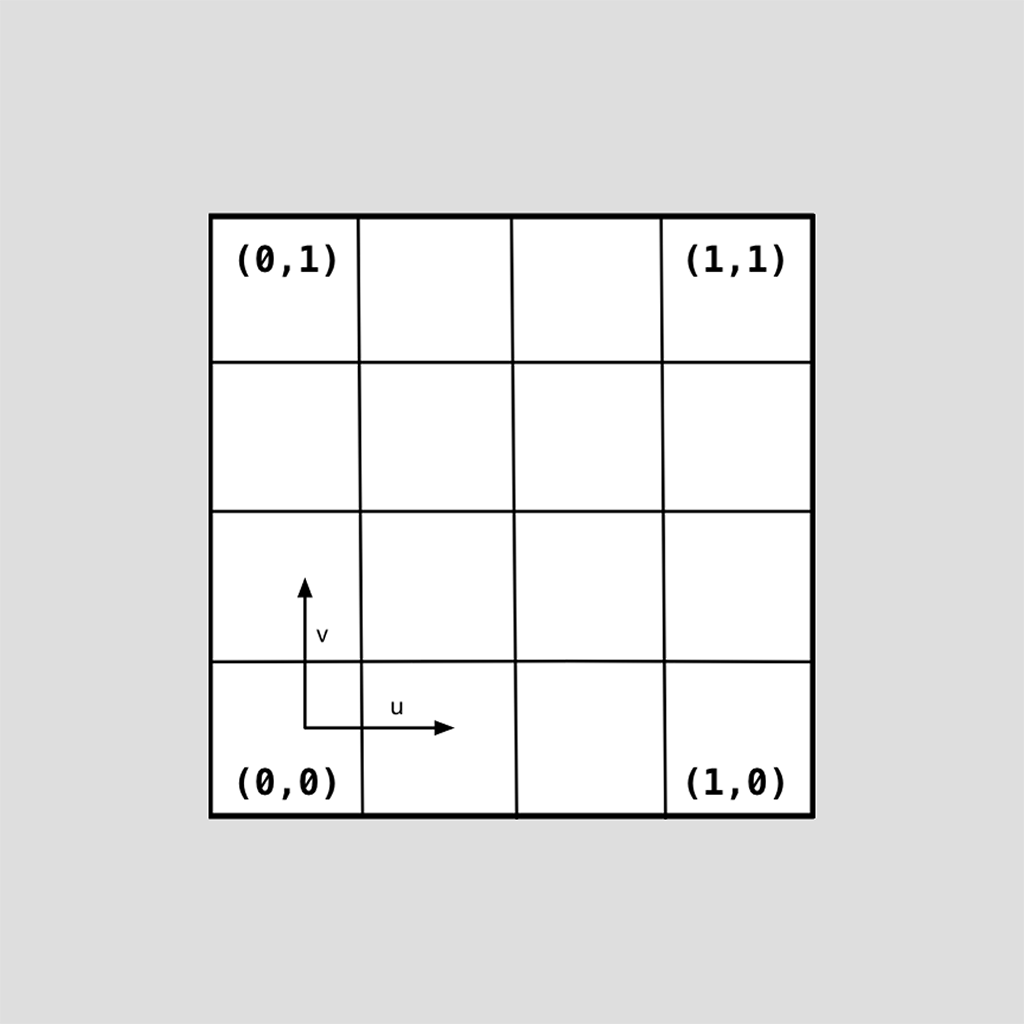
(u,v) 2D domain of a patch |
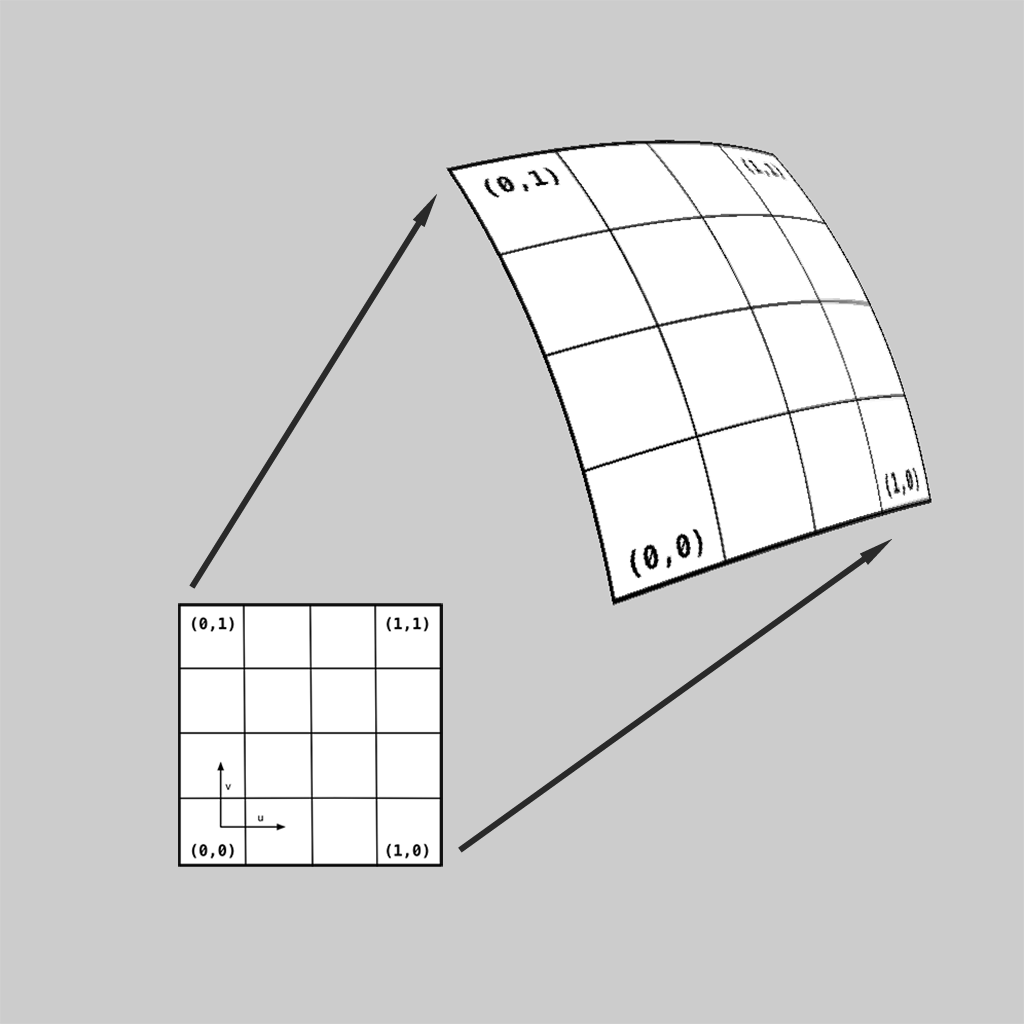
Mapping from (u,v) to (x,y,z) |
The points that control the shape of the surface are usually referred to as control points or control vertices, and the collection of the entire set defining a patch as the control mesh, the control hull, the control cage or simply the hull, the cage, etc. For the sake of brevity we will frequently use the term "cage", which serves us more generally later.
So a patch essentially consist of two entities: its control points and the surface affected by them.
The way the control points affect the surface is what makes the different types of patches unique. Even patches defined by the same number of points can have different behavior. Note that all 16 points of the B-Spline patch above are relatively far from the surface they define compared to the similar Bezier patch. The two patches in that example actually represent exactly the same piece of surface -- each with a set of control points having different effects on it. In mathematical terms, each control point has a "basis function" associated with it that affects the surface in a particular way when only that point is moved:
Bicubic B-Spline basis function |
Bicubic Bezier basis function |
It is these basis functions that often give rise to the names of the different patches.
There are pros and cons to these different properties of the control points of patches, which become more apparent as we assemble patches into piecewise surfaces.
Piecewise Surfaces
Piecewise parametric surfaces are collections of patches.
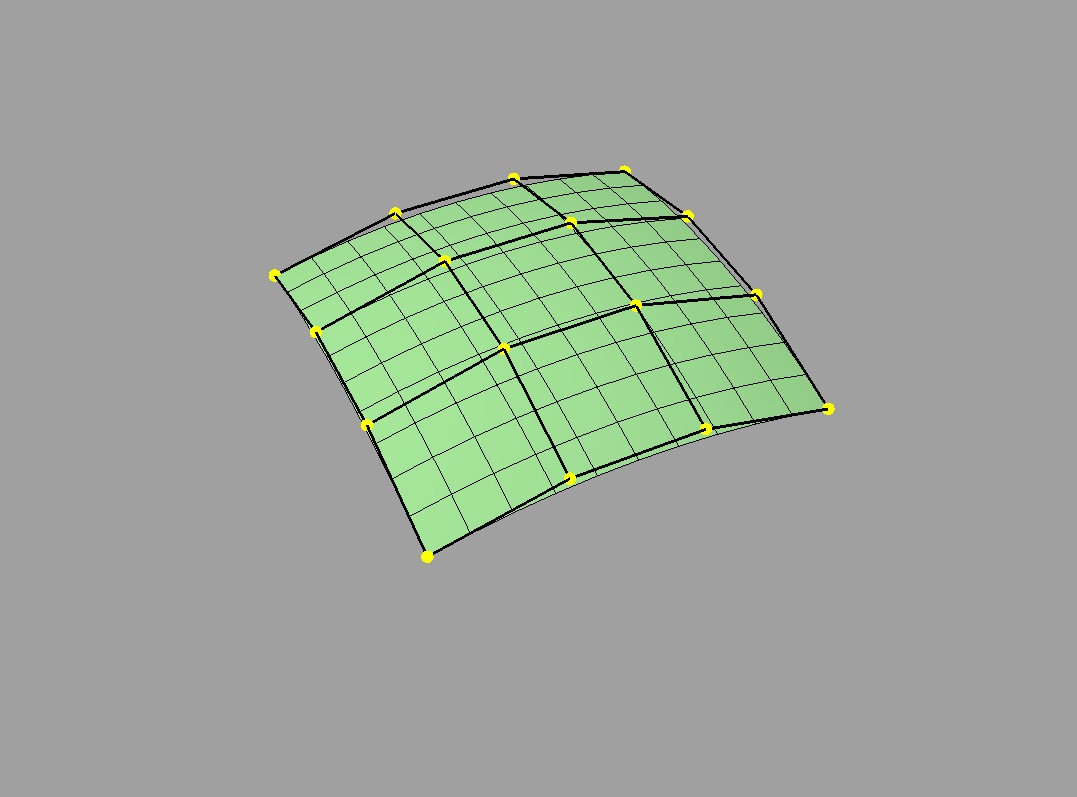
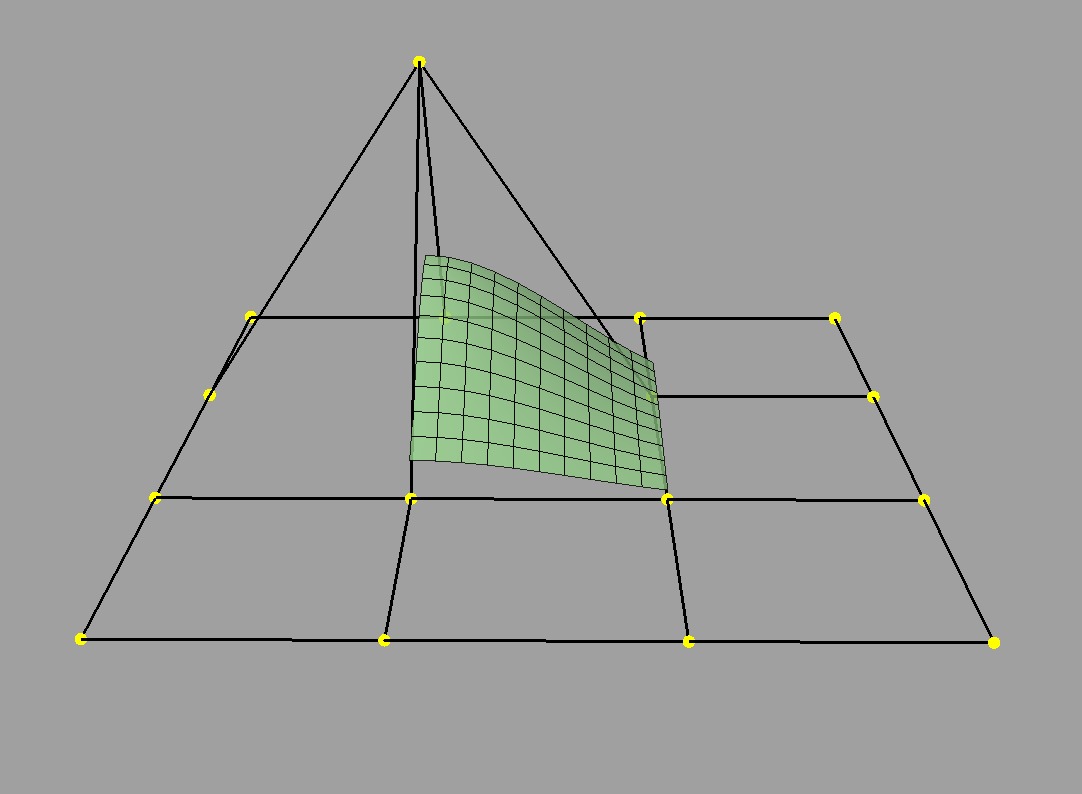
For rectangular patches, one of the simplest ways to construct a collection is to define a set of patches using a rectangular grid of control points:
Piecewise B-Spline surface |

Piecewise Bezier surface |
Note that we can overlap the points of adjacent B-spline patches. This overlapping means that moving one control point affects multiple patches -- but it also ensures that those patches always meet smoothly (this was a design intention and not true for other patch types). Adjacent Bezier patches only share points at their boundaries and coordinating the points across those boundaries to keep the surface smooth is possible, but awkward. This makes B-splines a more favorable surface representation for interactive modeling, but Bezier patches serve many other useful purposes.
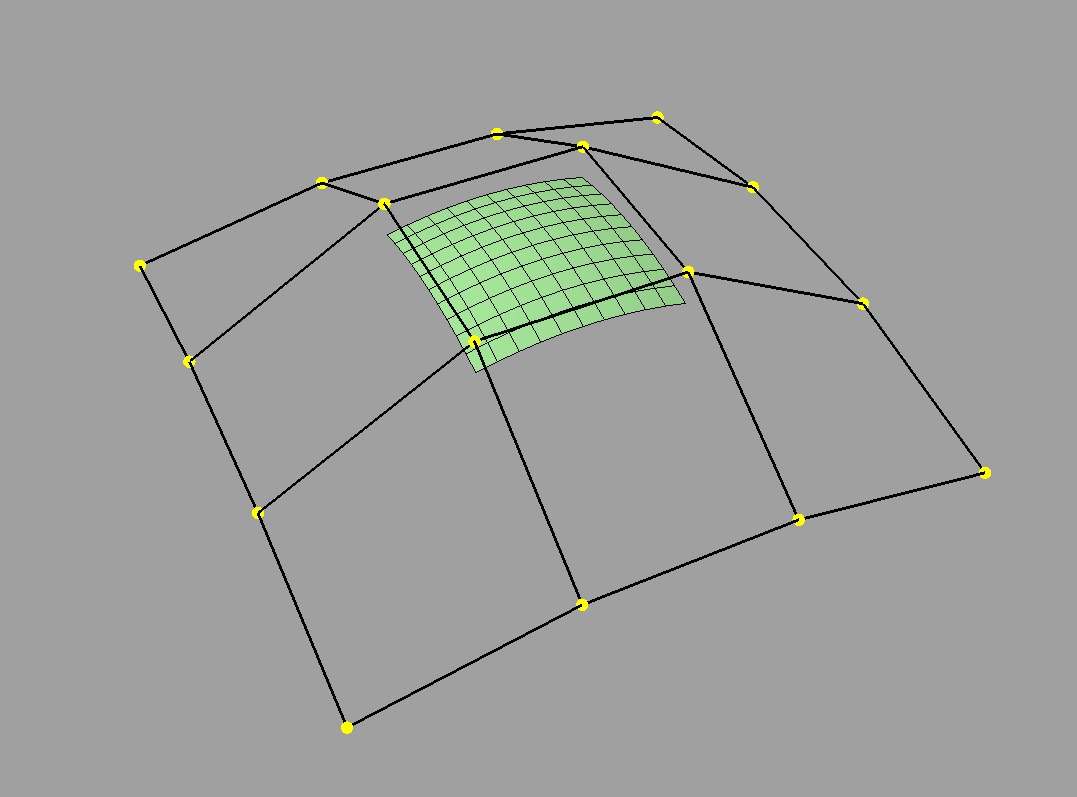
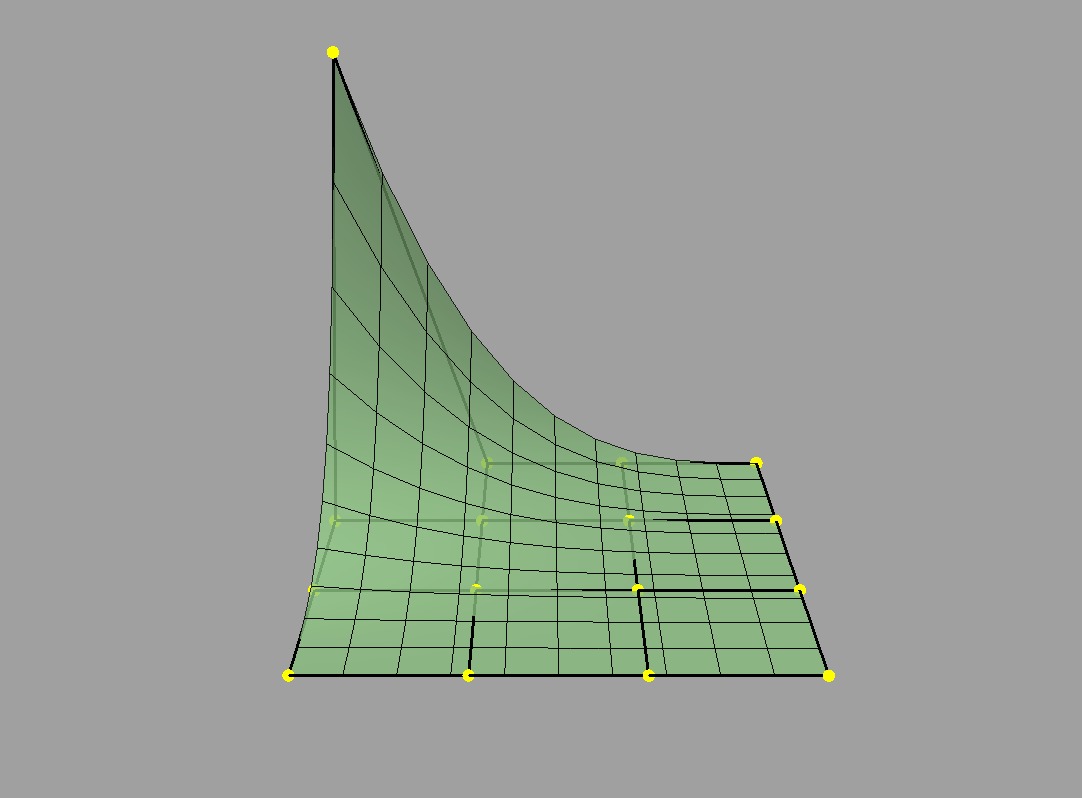
A more complicated B-spline surface:
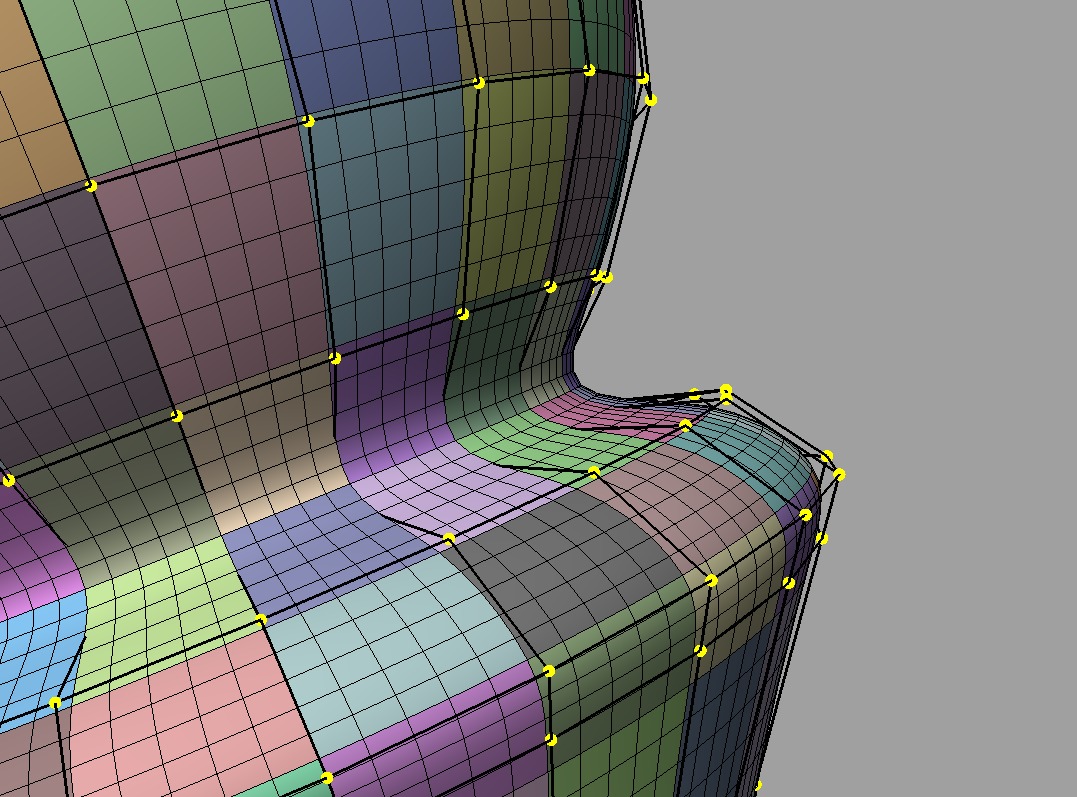
Part of a more complicated B-Spline surface |
Just as a patch consisted of a cage and a surface, the same is now true of the collection. The control cage is manipulated by a designer and the surface of each of the patches involved is displayed so they can assess its effect.
Arbitrary Topology
Piecewise surfaces discussed thus far have been restricted to collections of patches over regular grids of control points. There is a certain simplicity with rectangular parametric surfaces that is appealing, but a surface representation that supports arbitrary topology has many other advantages.
Rectangular parametric surfaces gained widespread adoption despite their topological limitations, and their popularity continues today in some areas. Complex objects often need many such surfaces to represent them and a variety of techniques have evolved to assemble them effectively, including "stitching" multiple surfaces together or cutting holes into them ("trimming"). These are complicated techniques, and while effective in some contexts (e.g. industrial design) they become cumbersome in others (e.g. animation and visual effects).
A single polygonal mesh can represent shapes with far more complexity than a single rectangular piecewise surface, but its faceted nature eventually becomes a problem.
Subdivision surfaces combine the topological flexibility of polygonal meshes with the underlying smoothness of piecewise parametric surfaces. Just as rectangular piecewise parametric surfaces have a collection of control points (its cage stored as a grid) and an underlying surface, subdivision surfaces also have a collection of control points (its cage stored as a mesh) and an underlying surface (often referred as its "limit surface").
Regular versus Irregular Features
A mesh contains the vertices and faces that form the cage for the underlying surface, and the topology of that mesh can be arbitrarily complex.
In areas where the faces and vertices of the mesh are connected to form rectangular grids, the limit surface becomes one of the rectangular piecewise parametric surfaces previously mentioned. These regions of the mesh are said to be "regular": they provide behavior familiar from the use of similar rectangular surfaces and their limit surface is relatively simple to deal with. All other areas are considered "irregular": they provide the desired topological flexibility and so are less familiar (and less predictable in some cases) and their limit surface can be much more complicated.
Irregular features come in a number of forms. The most widely referred to is an extra-ordinary vertex, i.e. a vertex which, in the case of a quad subdivision scheme like Catmull-Clark, does not have four incident faces.
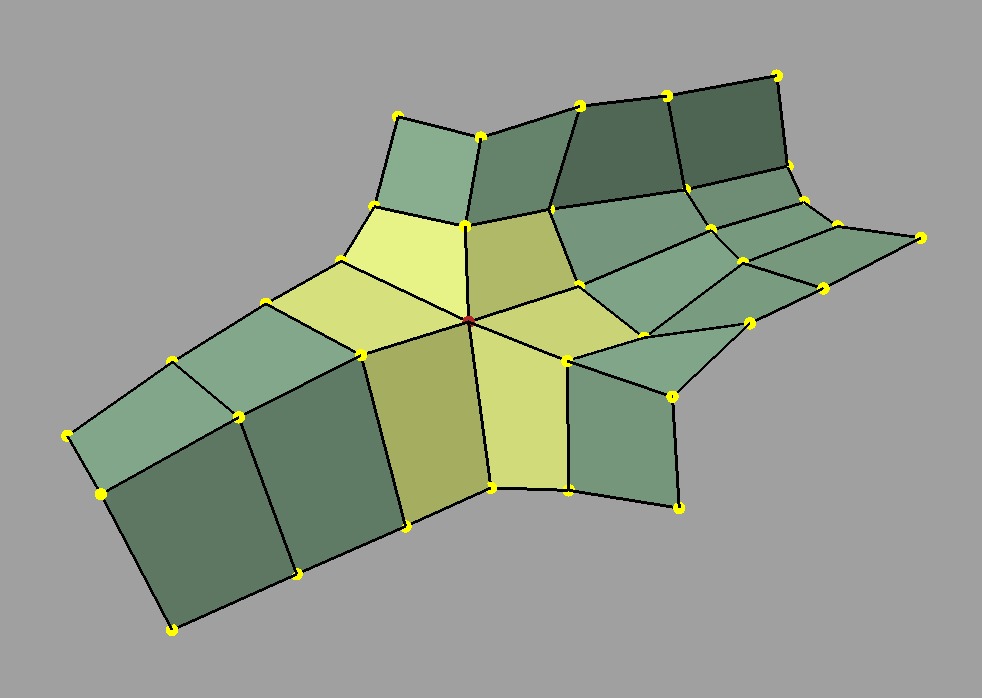
Irregular vertex and incident faces |

Regular and irregular regions of the surface |
The presence of these irregular features makes the limit surface around them similarly irregular, i.e. it cannot be represented as simply as it can for regular regions.
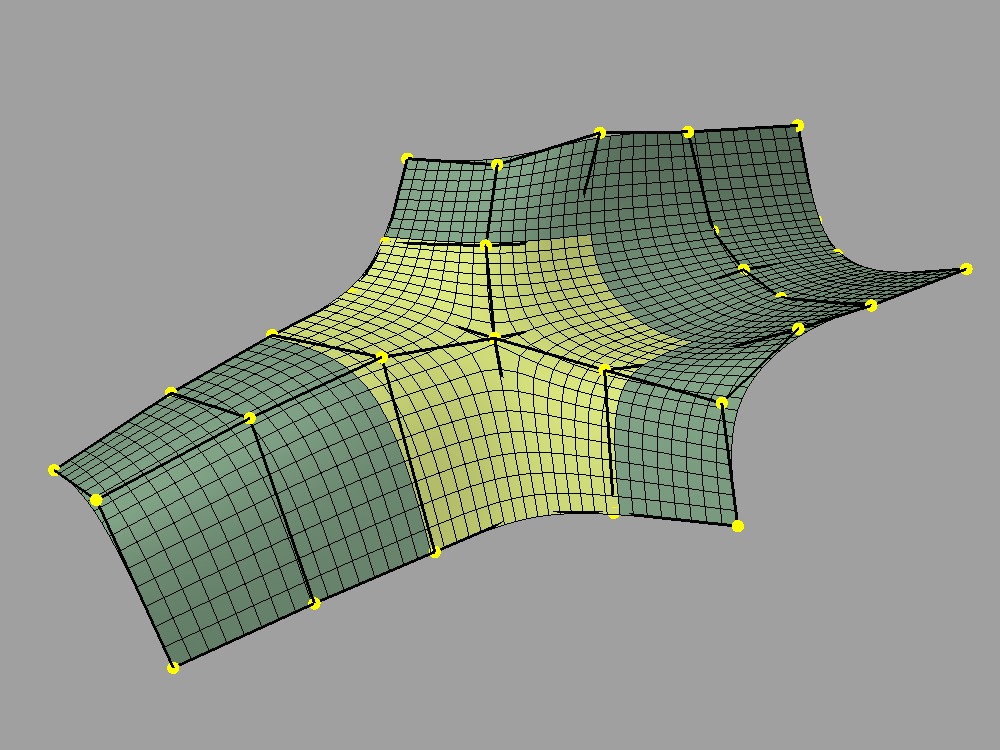
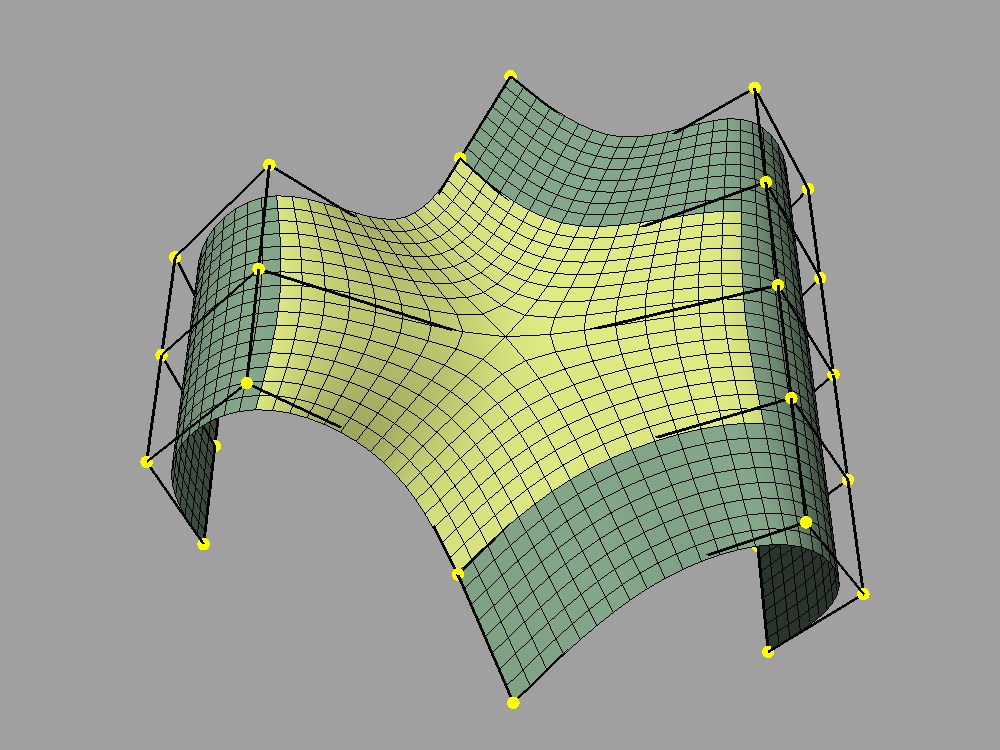
It's worth noting that irregular regions shrink in size and become more "isolated" as subdivision is applied. A face with a lot of extra-ordinary vertices around it makes for a very complicated surface, and isolating these features is a way to help deal with that complexity:
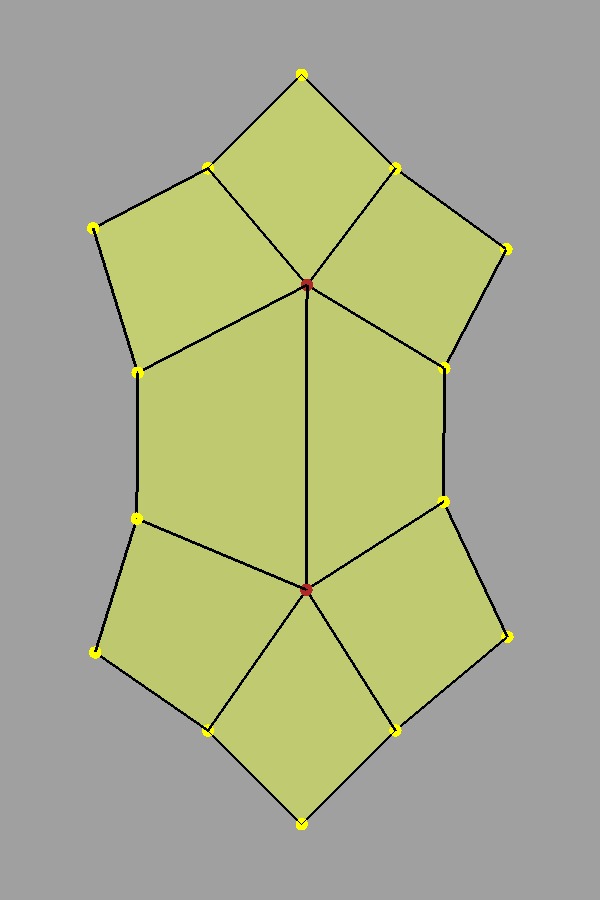
Two valence-5 vertices nearby |
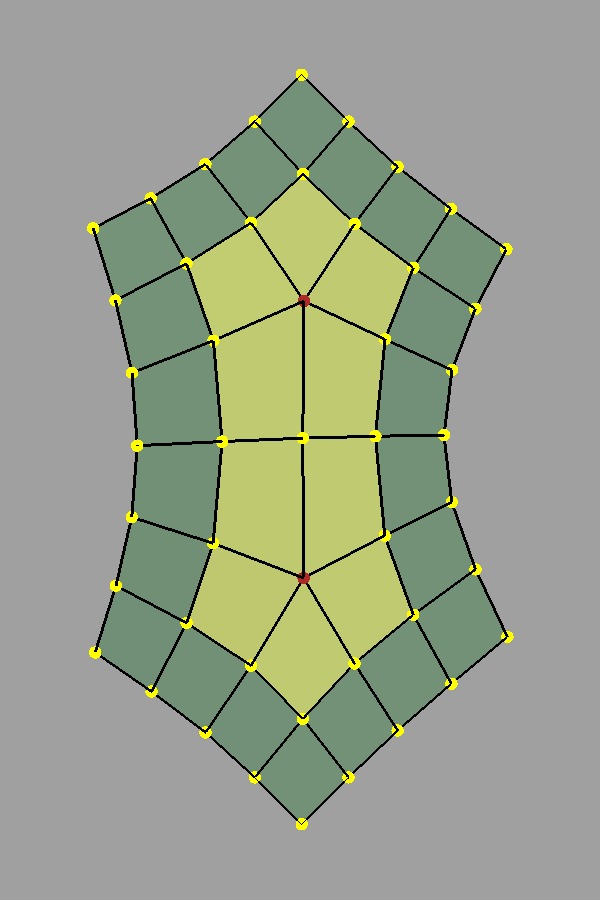
Isolation subdivided once |

Isolation subdivided twice |
It's generally necessary to perform some kind of local subdivision in these areas to break these pieces of surface into smaller, more manageable pieces, and the term "feature adaptive subdivision" has become popular in recent years to describe this process. Whether this is done explicitly or implicitly, globally or locally, what matters most is that there is an underlying piece of limit surface for each face -- albeit a potentially complicated one at an irregular feature -- that can be evaluated in much the same way as rectangular piecewise surfaces.
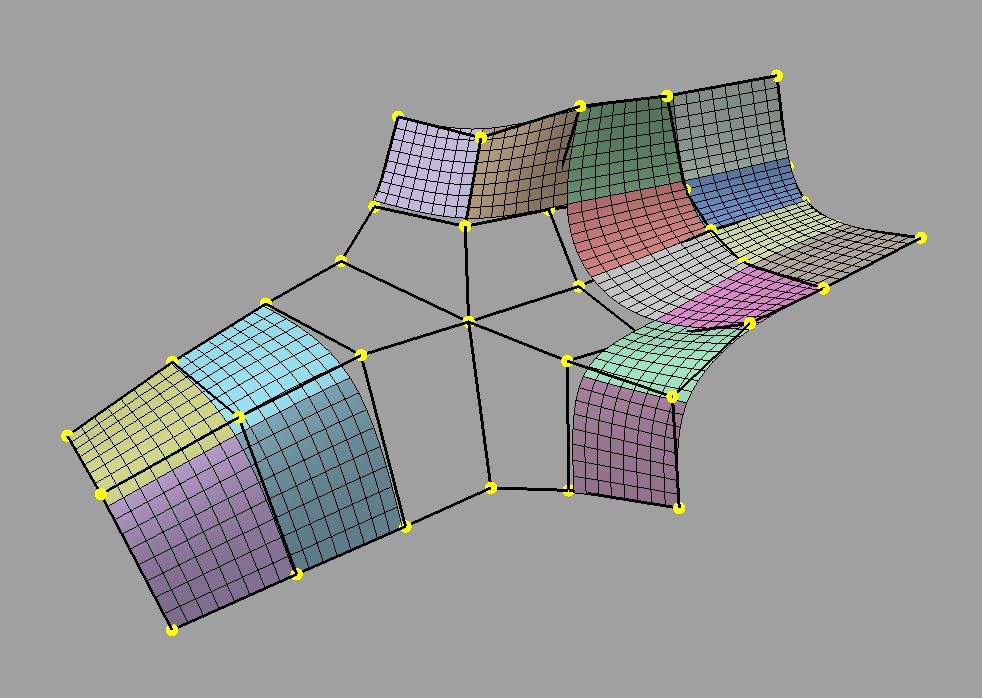
Patches of the regular regions |

Patches of the irregular region |
While supporting a smooth surface in these irregular areas is the main advantage of subdivision surfaces, both the complexity of the resulting surfaces and their quality are reasons to use them with care. When the topology is largely irregular, there is a higher cost associated with its surface, so minimizing irregularities is advantageous. And in some cases the surface quality, i.e. the perceived smoothness, of the irregular surfaces can lead to undesirable artefacts.
An arbitrary polygonal mesh will often not make a good subdivision cage, regardless of how good that polygonal mesh appears.
As with rectangular piecewise parametric surfaces, the cage should be shaped to affect the underlying surface it is intended to represent. See Modeling Tips for related recommendations.
Non-manifold Topology
Since the cage of a subdivision surface is stored in a mesh, and often manipulated in the same context as polygonal meshes, the topic of manifold versus non-manifold topology warrants some attention.
There are many definitions or descriptions of what distinguishes a manifold mesh from one that is not. These range from concise but abstract mathematical definitions to sets of examples showing manifold and non-manifold meshes -- all have their value and an appropriate audience. The following is not a strict definition but serves well to illustrate most local topological configurations that cause a mesh to be non-manifold.
Consider "standing" on the faces of a mesh and "walking" around each vertex in turn. Assuming a right-hand winding order of faces, stand on the side of the face in the positive normal direction. And when walking, step across each incident edge in a counter-clockwise direction to the next incident face.
For an interior vertex:
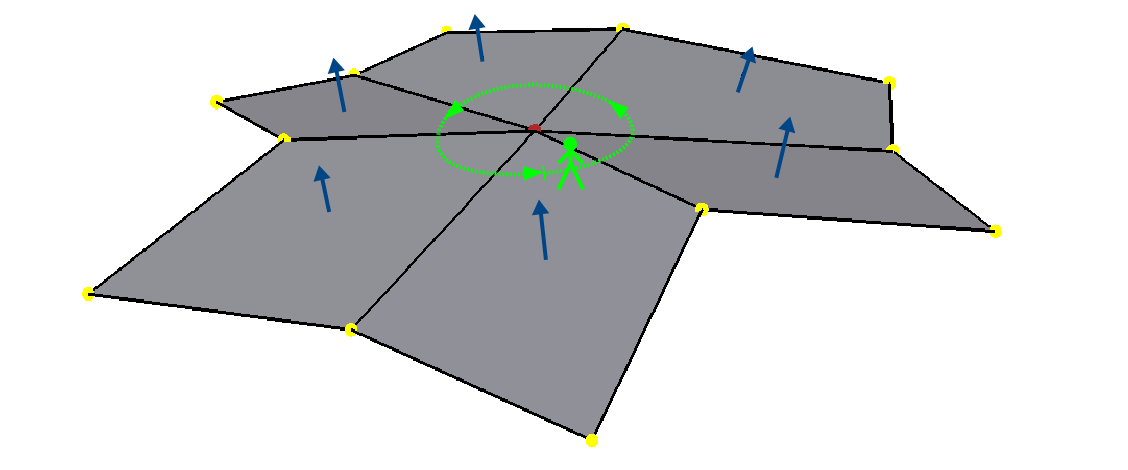
- start at the corner of any incident face
- walk around the vertex across each incident edge to the next unvisited face; repeat
- if you arrive back where you started and any incident faces or edges were not visited, the mesh is non-manifold
Similarly, for a boundary vertex:
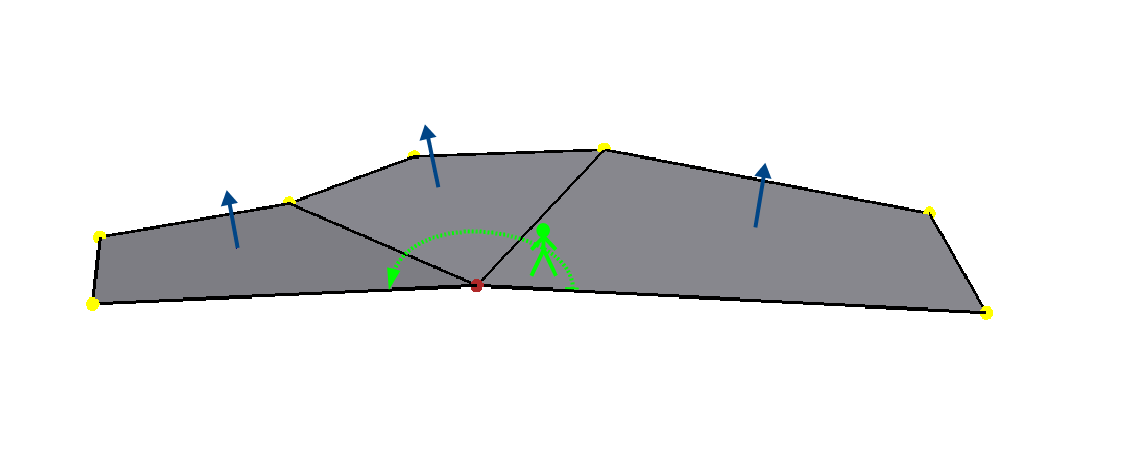
- start at the corner of the face containing the leading boundary edge
- walk around the vertex across each incident edge to the next unvisited face; repeat
- if you arrive at another boundary edge and any incident faces or edges were not visited, the mesh is non-manifold
If you can walk around all vertices this way and don't encounter any non-manifold features, the mesh is likely manifold.
Obviously if a vertex has no faces, there is nothing to walk around and this test can't succeed, so it is again non-manifold. All of the faces around a vertex should also be in the same orientation, otherwise two adjacent faces have normals in opposite directions and the mesh will be considered non-manifold, so we should really include that constraint when stepping to the next face to be more strict.
Consider walking around the indicated vertices of the following non-manifold meshes:
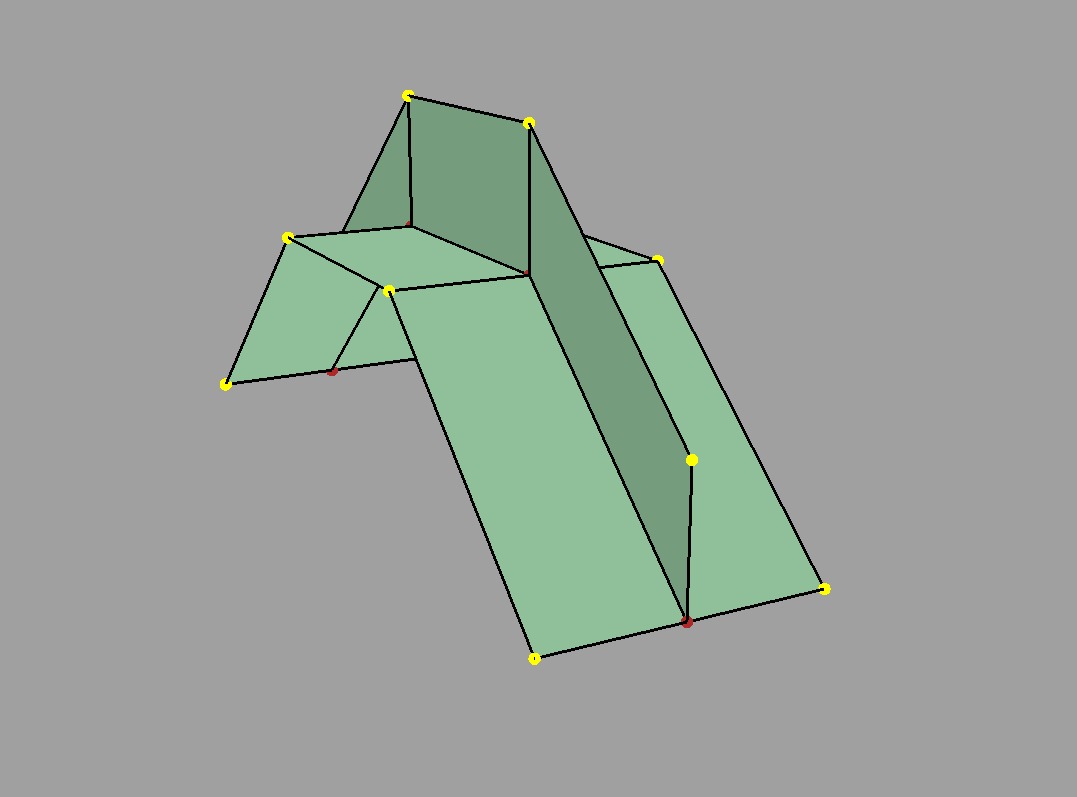
Edges with > 2 incident faces |
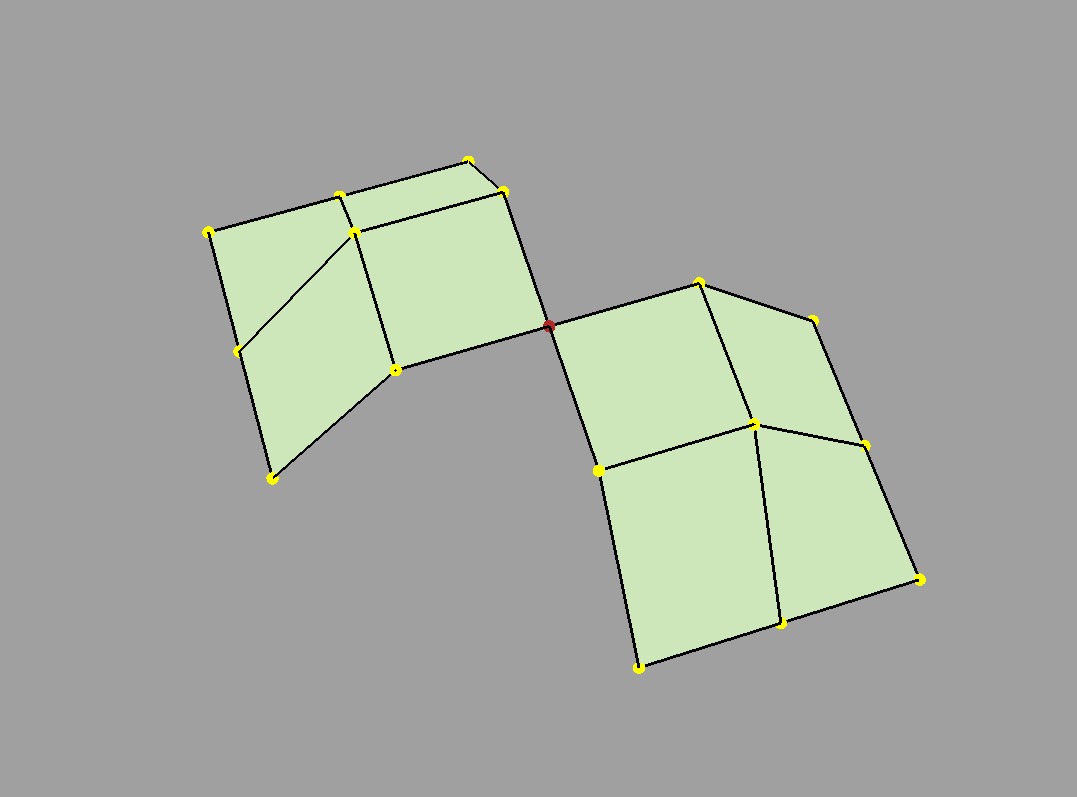
Faces sharing a vertex but no edges |
As mentioned earlier, many tools do not support non-manifold meshes, and in some contexts, e.g. 3D printing, they should be strictly avoided. Sometimes a manifold mesh may be desired and enforced as an end result, but the mesh may temporarily become non-manifold due to a particular sequence of modeling operations.
Rather than supporting or advocating the use of non-manifold meshes, OpenSubdiv strives to be robust in the presence of non-manifold features to simplify the usage of its clients -- sparing them the need for topological analysis to determine when OpenSubdiv can or cannot be used. Although subdivision rules are not as well standardized in areas where the mesh is not manifold, OpenSubdiv provides simple rules and a reasonable limit surface in most cases.
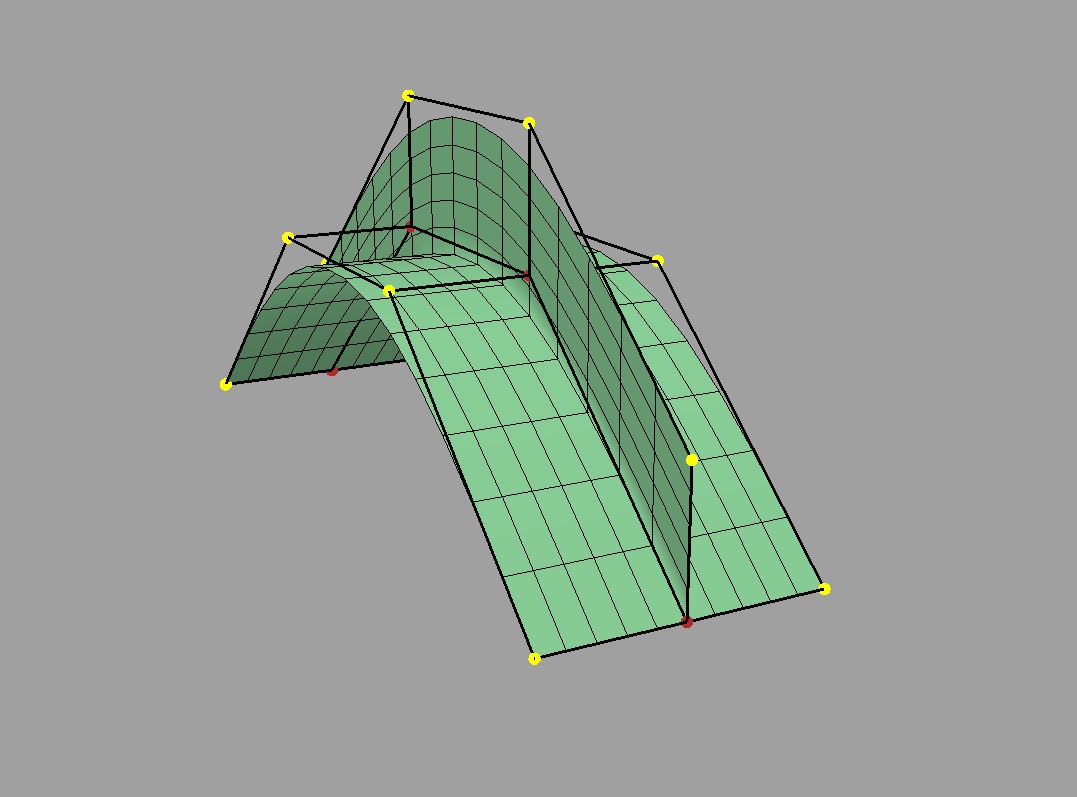
Surface around edges with > 2 incident faces |
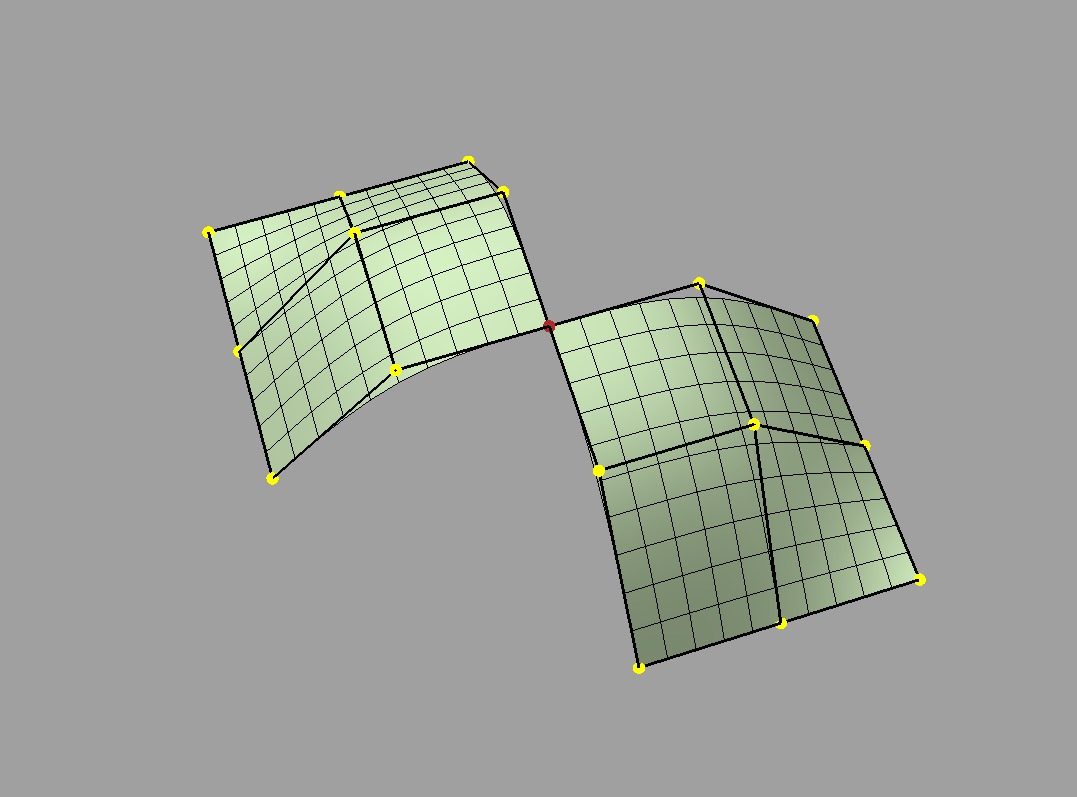
Surface for faces sharing a vertex but no edges |
As with the case of regular versus irregular features, since every face has a corresponding piece of surface associated with it -- whether locally manifold or not -- the term "arbitrary topology" can be said to include non-manifold topology.
Subdivision versus Tessellation
The preceding sections illustrate subdivision surfaces as piecewise parametric surfaces of arbitrary topology. As piecewise parametric surfaces, they consist of a cage and the underlying surface defined by that cage.
Two techniques used to display subdivision surfaces are subdivision and tessellation. Both have their legitimate uses, but there is an important distinction between them:
- subdivision operates on a cage and produces a refined cage
- tessellation operates on a surface and produces a discretization of that surface
The existence and relative simplicity of the subdivision algorithm makes it easy to apply repeatedly to approximate the shape of the surface, but with the result being a refined cage, that approximation is not always very accurate. When compared to a cage refined to a different level, or a tessellation that uses points evaluated directly on the limit surface, the discrepancies can be confusing.
Subdivision
Subdivision is the process that gives "subdivision surfaces" their name, but it is not unique to them. Being piecewise parametric surfaces, let's first look at subdivision in the context of the simpler parametric patches that comprise them.
Subdivision is a special case of refinement, which is key to the success of some of the most widely used types of parametric patches and their aggregate surfaces. A surface can be "refined" when an algorithm exists such that more control points can be introduced while keeping the shape of the surface exactly the same. For interactive and design purposes, this allows a designer to introduce more resolution for finer control without introducing undesired side effects in the shape. For more analytical purposes, it allows the surface to be broken into pieces, often adaptively, while being faithful to the original shape.
One reason why both B-spline and Bezier patches are so widely used is that both of them can be refined. Uniform subdivision -- the process of splitting each of the patches in one or both of its directions -- is a special case of refinement that both of these patch types support:
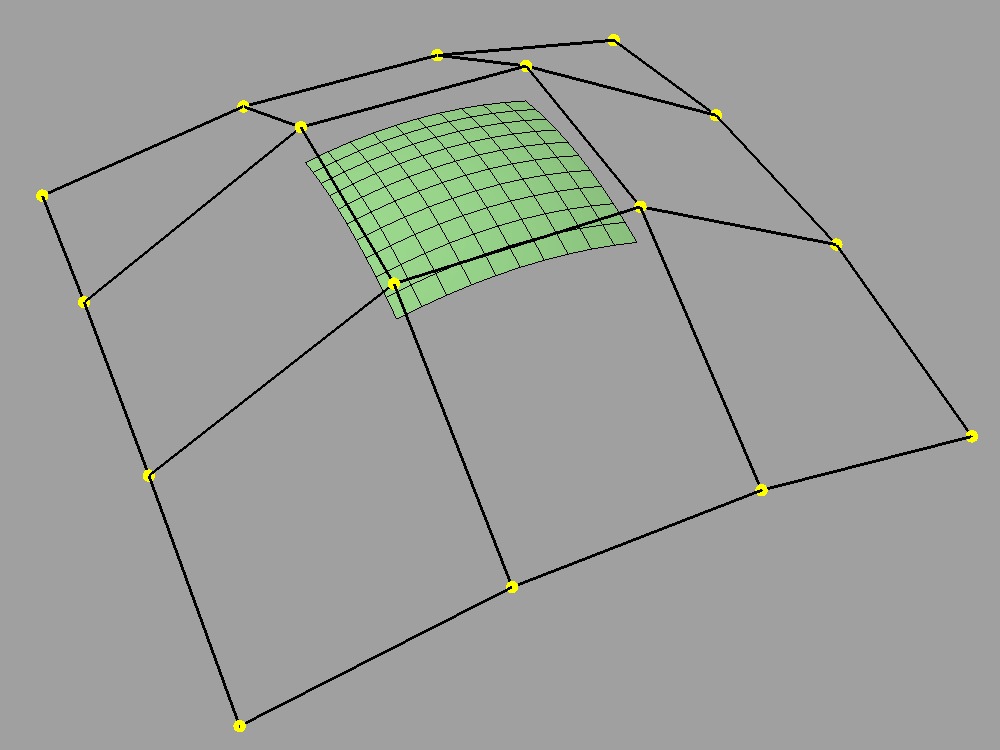
B-Spline surface and its cage |
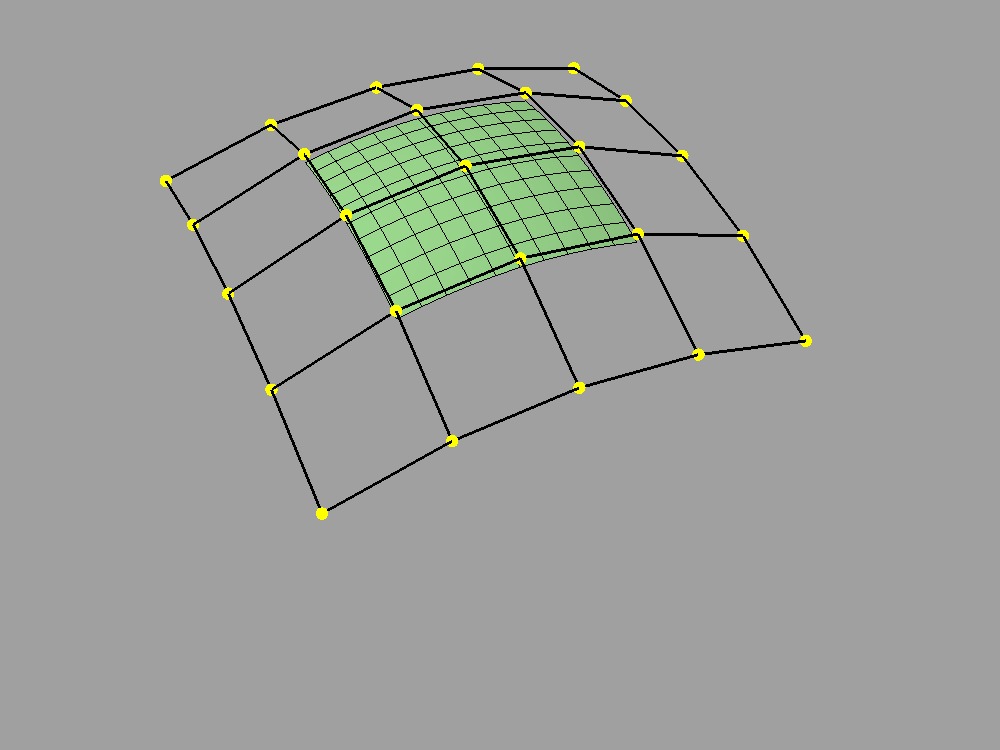
Cage subdivided 1x |
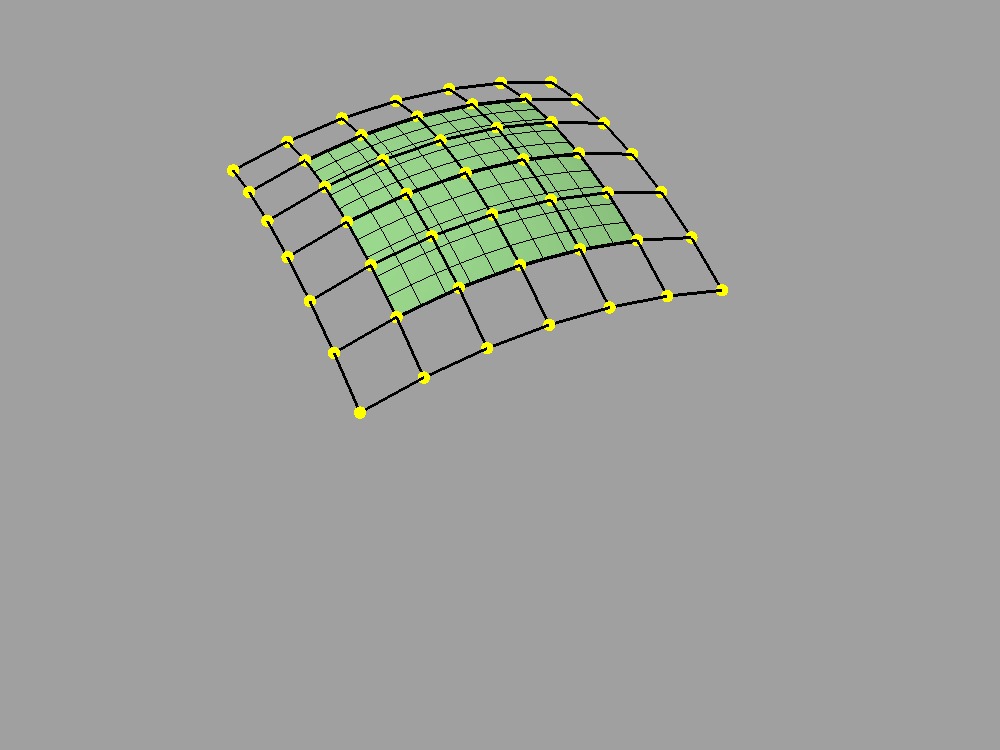
Cage subdivided 2x |
In the cases illustrated above for B-Splines, the uniformly refined cages produce the same limit surface as the original (granted in more pieces). So it is fair to say that both uniform B-splines and Bezier surfaces are subdivision surfaces.
The limit surface remains the same with the many more control points (roughly 4x with each iteration of subdivision), and those points are closer to (but not on) the surface. It may be tempting to use these new control points to represent the surface, but using the same number of points evaluated at corresponding uniformly spaced parametric locations on the surface is usually simpler and more effective.
Note also that points of the cage typically do not have any normal vectors associated with them, though we can evaluate normals explicitly for arbitrary locations on the surface just as we do for position. So if displaying a cage as a shaded surface, normal vectors at each of the control points must be contrived. Both the positions and normals of the points on the finer cage are therefore both approximations.
For more general subdivision surfaces, the same is true. Subdivision will refine a mesh of arbitrary topology, but the resulting points will not lie on the limit surface and any normal vectors contrived from and associated with these points will only be approximations to those of the limit surface.
Tessellation
There is little need to use subdivision to approximate a parametric surface when it can be computed directly, i.e. it can be tessellated. We can evaluate at arbitrary locations on the surface and connect the resulting points to form a tessellation -- a discretization of the limit surface -- that is far more flexible than the results achieved from uniform subdivision:
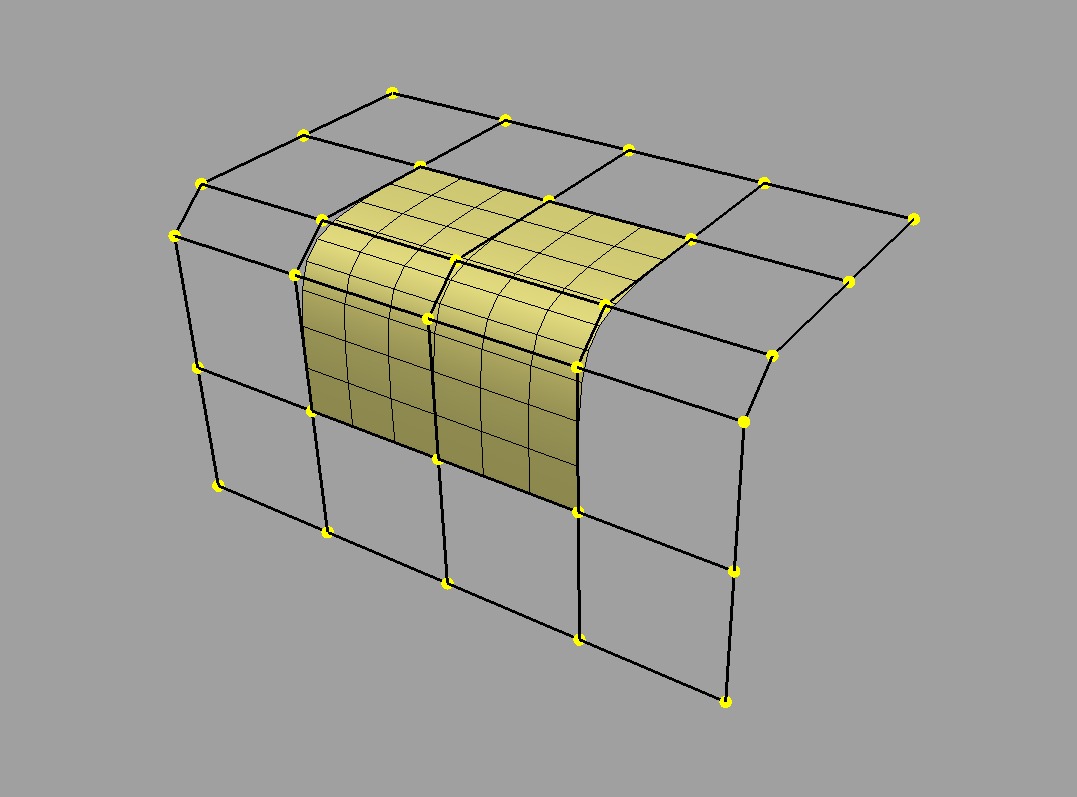
Uniform (3x3) tessellation of B-spline surface |
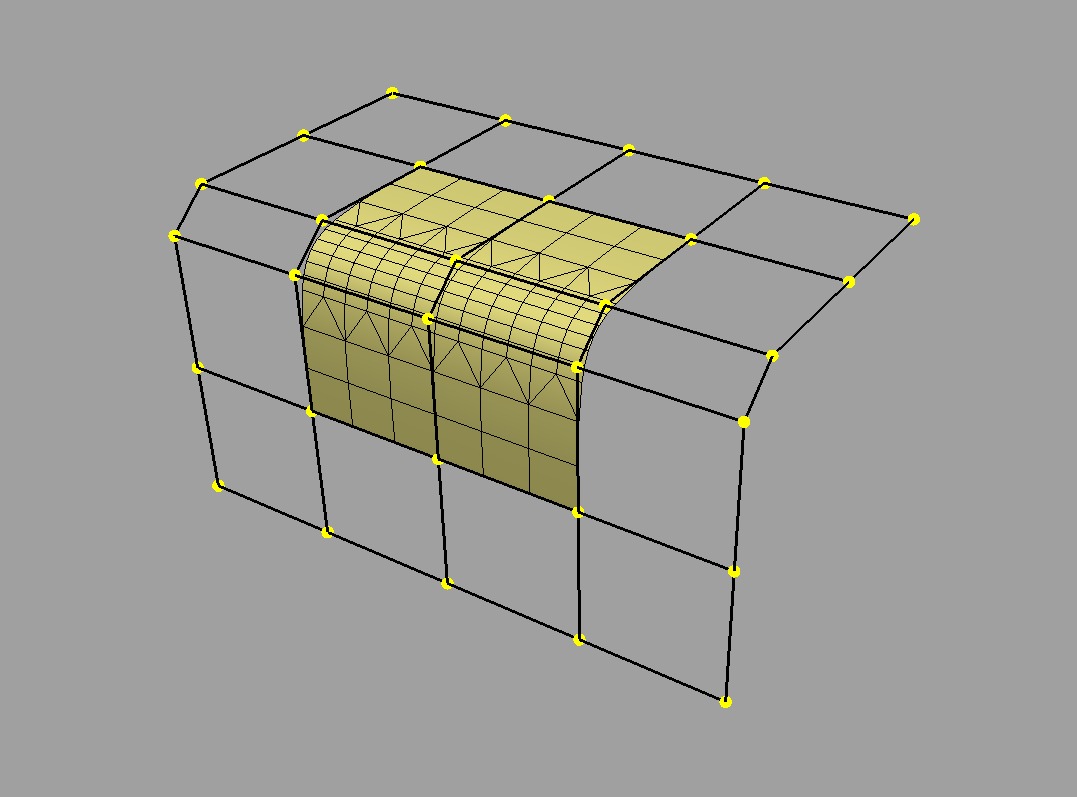
Curvature-adaptive tessellation of B-spline surface |
For a simple parametric surface, the direct evaluation of the limit surface is also simple, but for more complicated subdivision surfaces of arbitrary topology, this is less the case. The lack of a clear understanding of the relationship between the limit surface and the cage has historically lead to many applications avoiding tessellation.
It's worth mentioning that subdivision can be used to generate a tessellation even when the limit surface is not available for direct evaluation. The recursive nature of subdivision does give rise to formulae that allow a point on the limit surface to be computed that corresponds to each point of the cage. This process is often referred to as "snapping" or "pushing" the points of the cage onto the limit surface.
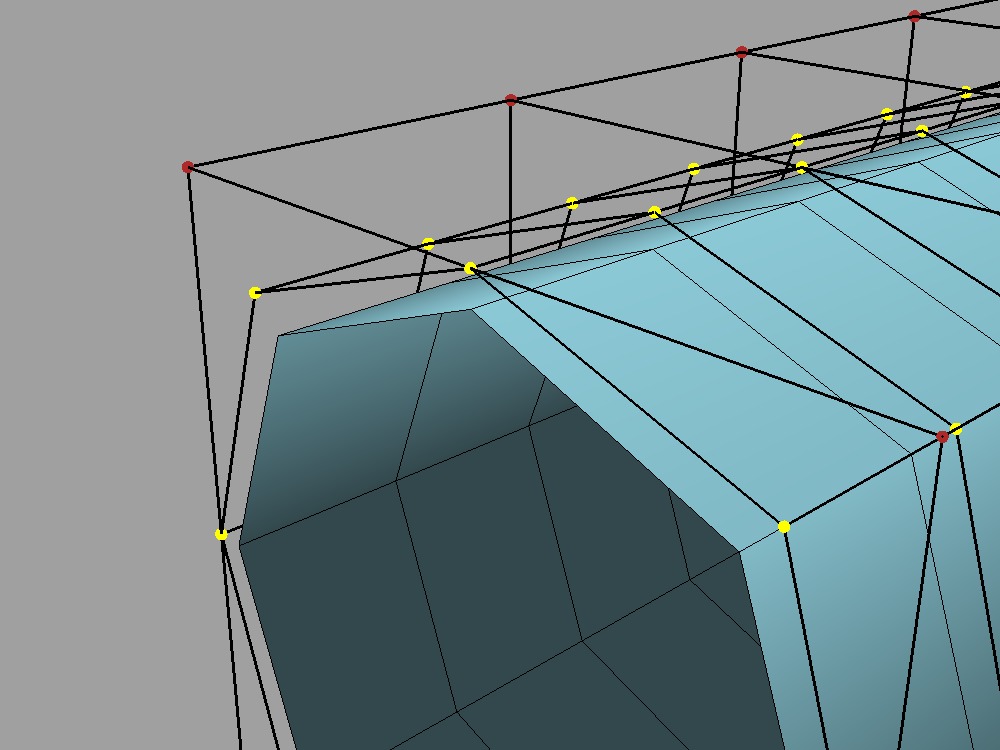
Subdivided 1x and snapped to limit surface |

Subdivided 2x and snapped to limit surface |
Since the end result is a connected set of points on the limit surface, this forms a tessellation of the limit surface, and we consider it a separate process to subdivision (though it does make use of it). The fact that such a tessellation might have been achieved using subdivision is indistinguishable from the final result -- the same tessellation might just as easily have been generated by evaluating limit patches of the cage uniformly 2x, 4x, 8x, etc. along each edge.
Which to Use?
Subdivision is undeniably useful in creating finer cages to manipulate the surface, but tessellation is preferred for displaying the surface when the patches are available for direct evaluation. There was a time when global refinement was pursued in limited circles as a way of rapidly evaluating parametric surfaces along isoparametric lines, but patch evaluation, i.e. tessellation, generally prevails.
Considerable confusion has arisen due the way the two techniques have been employed and presented when displaying the shape in end-user applications. One can argue that if an application displays a representation of the surface that is satisfactory for its purposes, then it is not necessary to burden the user with additional terminology and choices. But when two representations of the same surface differ considerably between two applications, the lack of any explanation or control leads to confusion.
As long as applications make different choices on how to display the surface, we seek a balance between simplicity and control. Since subdivided points do not lie on the limit surface, it is important to make it clear to users when subdivision is being used instead of tessellation. This is particularly true in applications where the cage and the surface are displayed in the same style as there is no visual cue for users to make that distinction.
Mesh Data and Topology
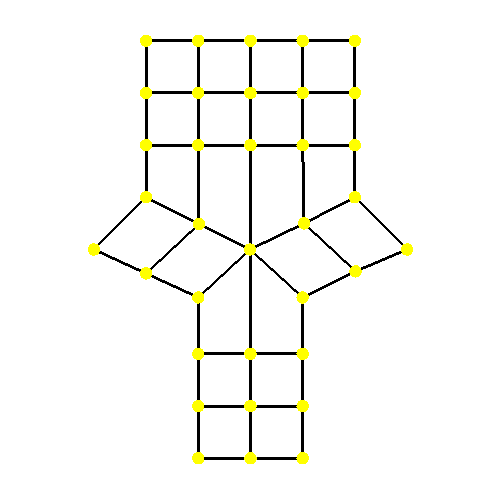
The ability of subdivision surfaces to support arbitrary topology leads to the use of meshes to store both the topology of the cage and the data values associated with its control points, i.e. its vertices. The shape of a mesh, or the subdivision surface that results from it, is a combination of the topology of the mesh and the position data associated with its vertices.
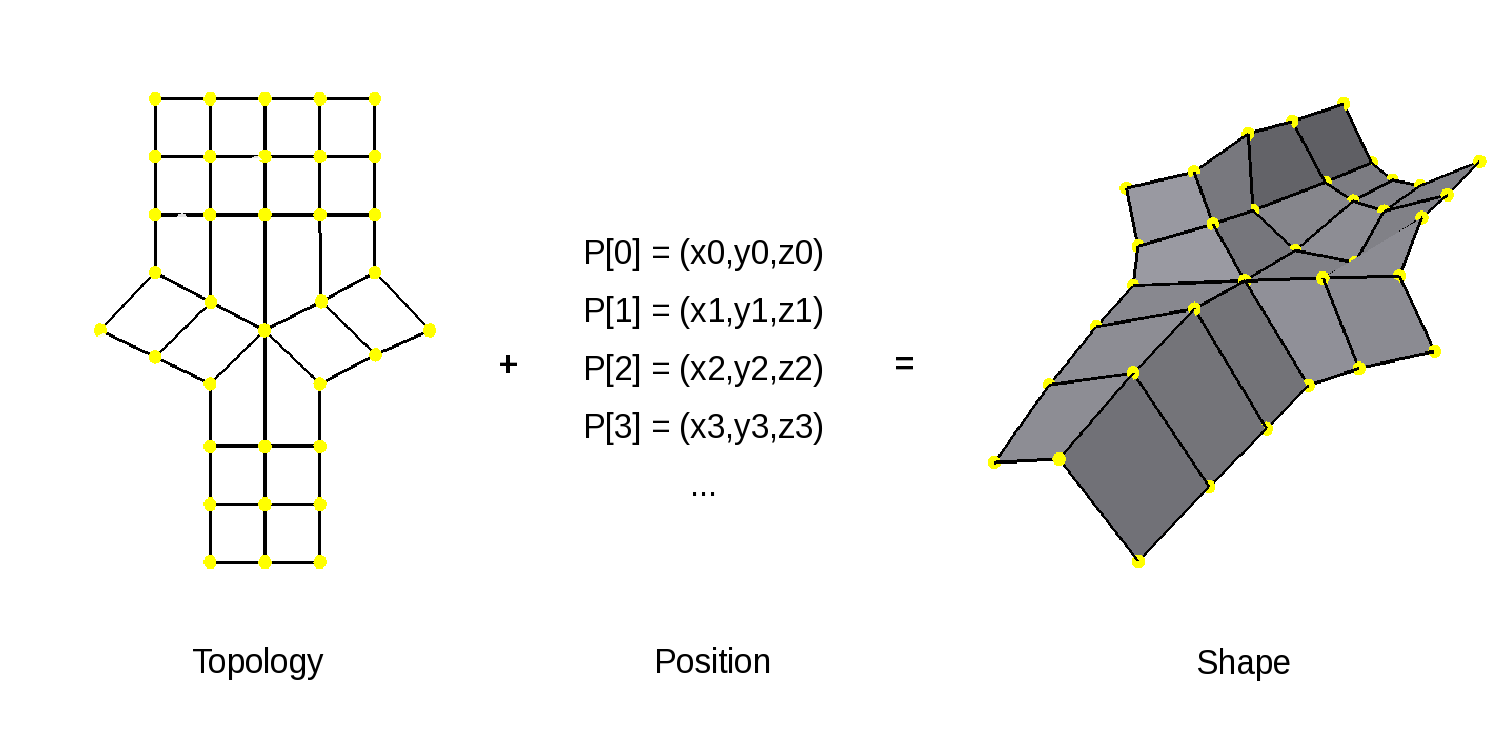
When dealing with meshes there are advantages to separating the topology from the data, and this is even more important when dealing with subdivision surfaces. The "shape" referred to above is not just the shape of the mesh (the cage in this case) but could be the shape of a refined cage or the limit surface. By observing the roles that both the data and topology play in operations such as subdivision and evaluation, significant advantages can be gained by managing data, topology and the associated computations accordingly.
While the main purpose of subdivision surfaces is to use position data associated with the vertices to define a smooth, continuous limit surface, there are many cases where non-positional data is associated with a mesh. That data may often be interpolated smoothly like position, but often it is preferred to interpolate it linearly or even make it discontinuous along edges of the mesh. Texture coordinates and color are common examples here.
Other than position, which is assigned to and associated with vertices, there are no constraints on how arbitrary data can or should be associated or interpolated. Texture coordinates, for example, can be assigned to create a completely smooth limit surface like the position, linearly interpolated across faces, or even made discontinuous between them. There are, however, consequences to consider -- both in terms of data management and performance -- which are described below as the terminology and techniques used to achieve each are defined.
Separating Data from Topology
While the topology of meshes used to store subdivision surfaces is arbitrarily complex and variable, the topology of the parametric patches that make up its limit surface are simple and fixed. Bicubic B-Spline and Bezier patches are both defined by a simple 4x4 grid of control points and a set of basis functions for each point that collectively form the resulting surface.
For such a patch, the position at a given parametric location is the result of the combination of position data associated with its control points and the weights of the corresponding basis functions (weights being the values of basis functions evaluated at a parametric location). The topology and the basis functions remain the same, so we can make use of the weights independent of the data. If the positions of the control points change, we can simply recombine the new position data with the weights that we just used and apply the same combination.

|
|

|
| The fixed topology of a parametric patch and two shapes resulting from two sets of positions. | ||
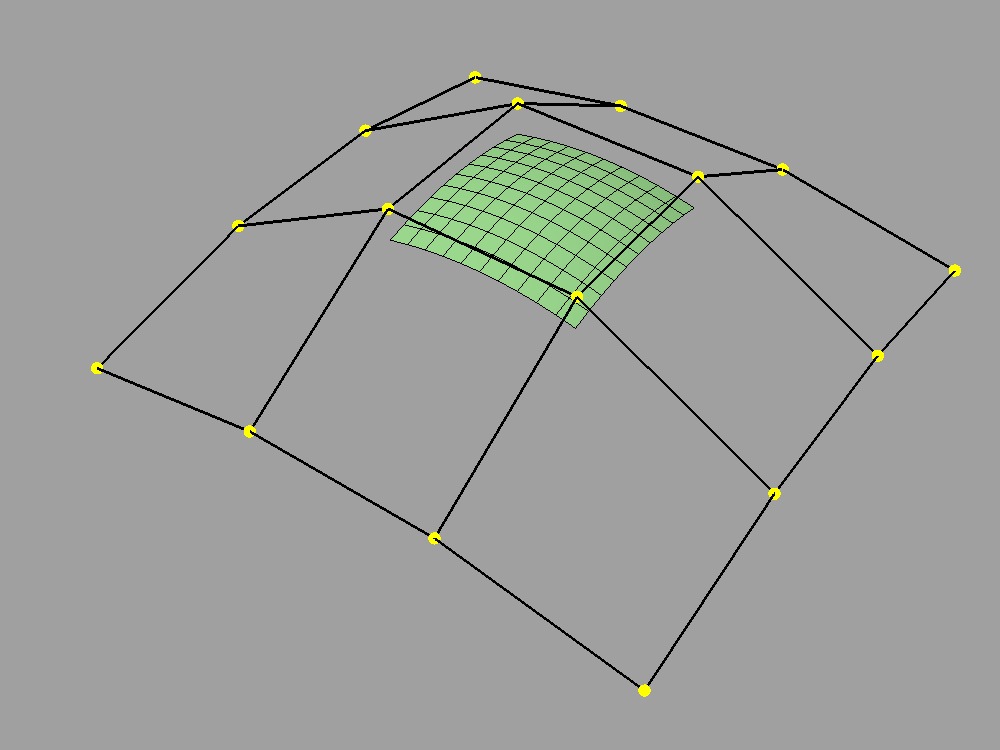
Similarly, for a piecewise surface, the position at a given parametric location is the result of the single patch containing that parametric location evaluated at the given position. The control points involved are the subset of control points associated with that particular patch. If the topology of the surface is fixed, so too is the topology of the collection of patches that comprise that surface. If the positions of those control points change, we can recombine the new position data with the same weights for the subset of points associated with the patch.
|
|
|
| More complex but fixed topology of a surface and two shapes resulting from two sets of positions. | ||
This holds for a piecewise surface of arbitrary topology. Regardless of how complex the topology, as long as it remains fixed (i.e. relationships between vertices, edges and faces does not change (or anything other settings affecting subdivision rules)), the same techniques apply.
This is just one example of the value of separating computations involving topology from those involving the data. Both subdivision and evaluation can be factored into steps involving topology (computing the weights) and combining the data separately.

|

|

|
| Three shapes resulting from three sets of positions for a mesh of fixed topology. | ||
When the topology is fixed, enormous savings are possible by pre-computing information associated with the topology and organizing the data associated with the control points in a way that can be efficiently combined with it. This is key to understanding some of the techniques used to process subdivision surfaces.
For a mesh of arbitrary topology, the control points of the underlying surface are the vertices, and position data associated with them is most familiar. But there is nothing that requires that the control points of a patch have to represent position -- the same techniques apply regardless of the type of data involved.
Vertex and Varying Data
The most typical and fundamental operation is to evaluate a position on the surface, i.e. evaluate the underlying patches of the limit surface using the (x,y,z) positions at the vertices of the mesh. Given a parametric (u,v) location on one such patch, the data-independent evaluation method first computes the weights and then combines the (x,y,z) vertex positions resulting in an (x,y,z) position at that location. But the weights and their combination can be applied to any data at the vertices, e.g. color, texture coordinates or anything else.
Data associated with the vertices that is interpolated this way, including position, is said to be "vertex" data or to have "vertex" interpolation. Specifying other data as "vertex" data will result in it being smoothly interpolated in exactly the same way (using exactly the same weights) as the position. So to capture a simple 2D projection of the surface for texture coordinates, 2D values matching the (x,y) of the positions would be used.
If linear interpolation of data associated with vertices is desired instead, the data is said to be "varying" data or to have "varying" interpolation. Here the non-linear evaluation of the patches defining the smooth limit surface is ignored and weights for simple linear interpolation are used. This is a common choice for texture coordinates as evaluation of texture without the need of bicubic patches is computationally cheaper. The linear interpolation will not capture the smoothness required of a true projection between the vertices, but both vertex and varying interpolation have their uses.
Projected texture smoothly interpolated from vertex data |

Projected texture linearly interpolated from varying data |
Since both vertex and varying data is associated with vertices (a unique value assigned to each), the resulting surface will be continuous -- piecewise smooth in the case of vertex data and piecewise linear in the case of varying.
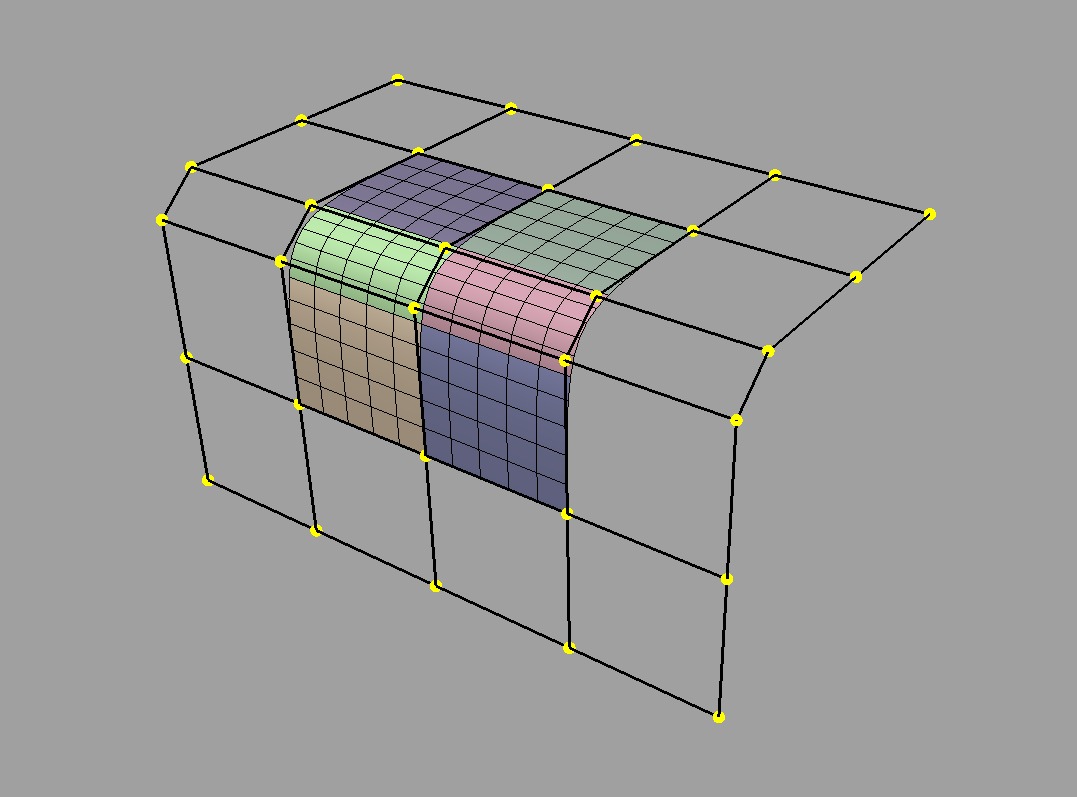
Face-Varying Data and Topology
In order to support discontinuities in data on the surface, unlike vertex and varying data, there must be multiple values associated with vertices, edges and/or faces, in order for a discontinuity to exist.
Discontinuities are made possible by assigning values to the corners of faces, similar to the way in which vertices are assigned to the corners of faces when defining the topology of the mesh. Recalling the assignment of vertices to faces:
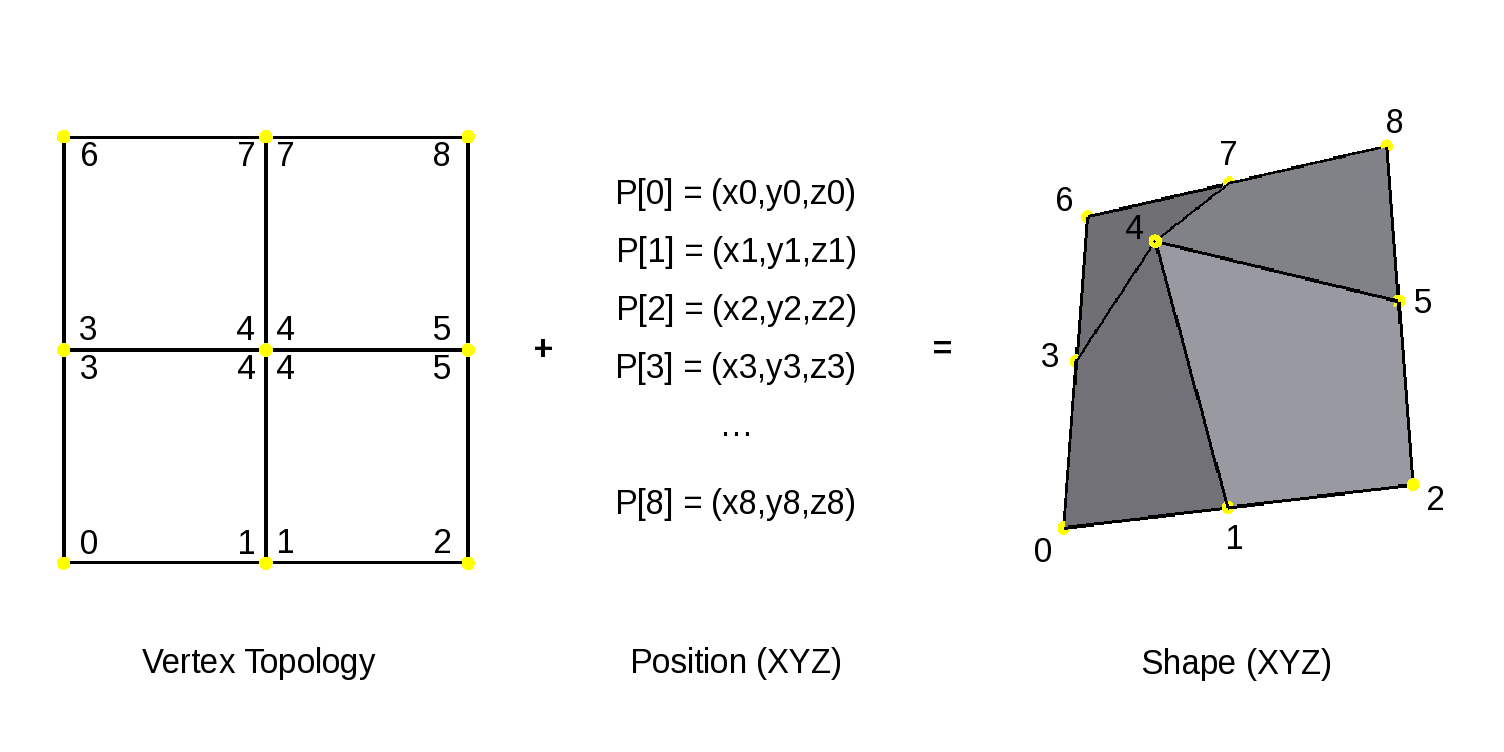
Vertex indices are assigned to all corners of each face as part of mesh construction and are often referred to as the face-vertices of an individual face or the mesh. All face-vertices that share the same vertex index will be connected by that vertex and share the same vertex data associated with it.
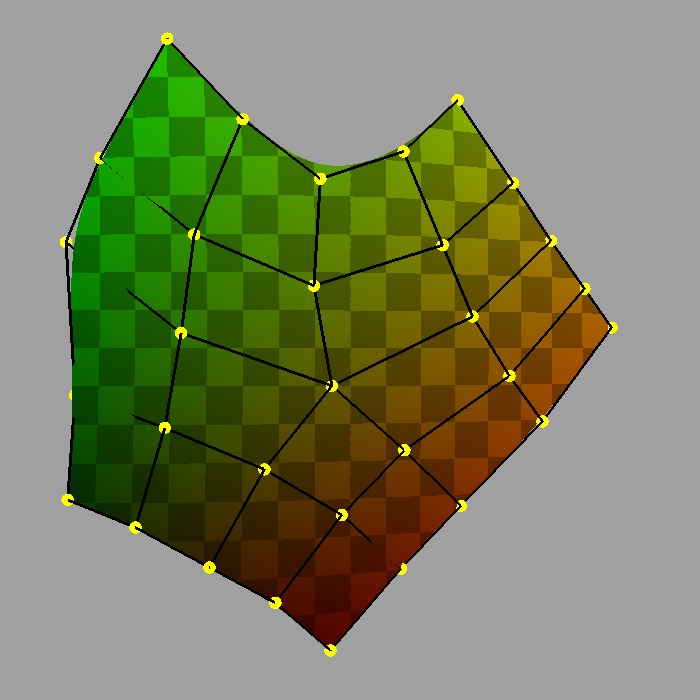
By assigning a different set of indices to the face-vertices -- indices not referring to the vertices but some set of data to be associated with the corners of each face -- corners that share the same vertex no longer need to share the same data value and the data can be made discontinuous between faces:
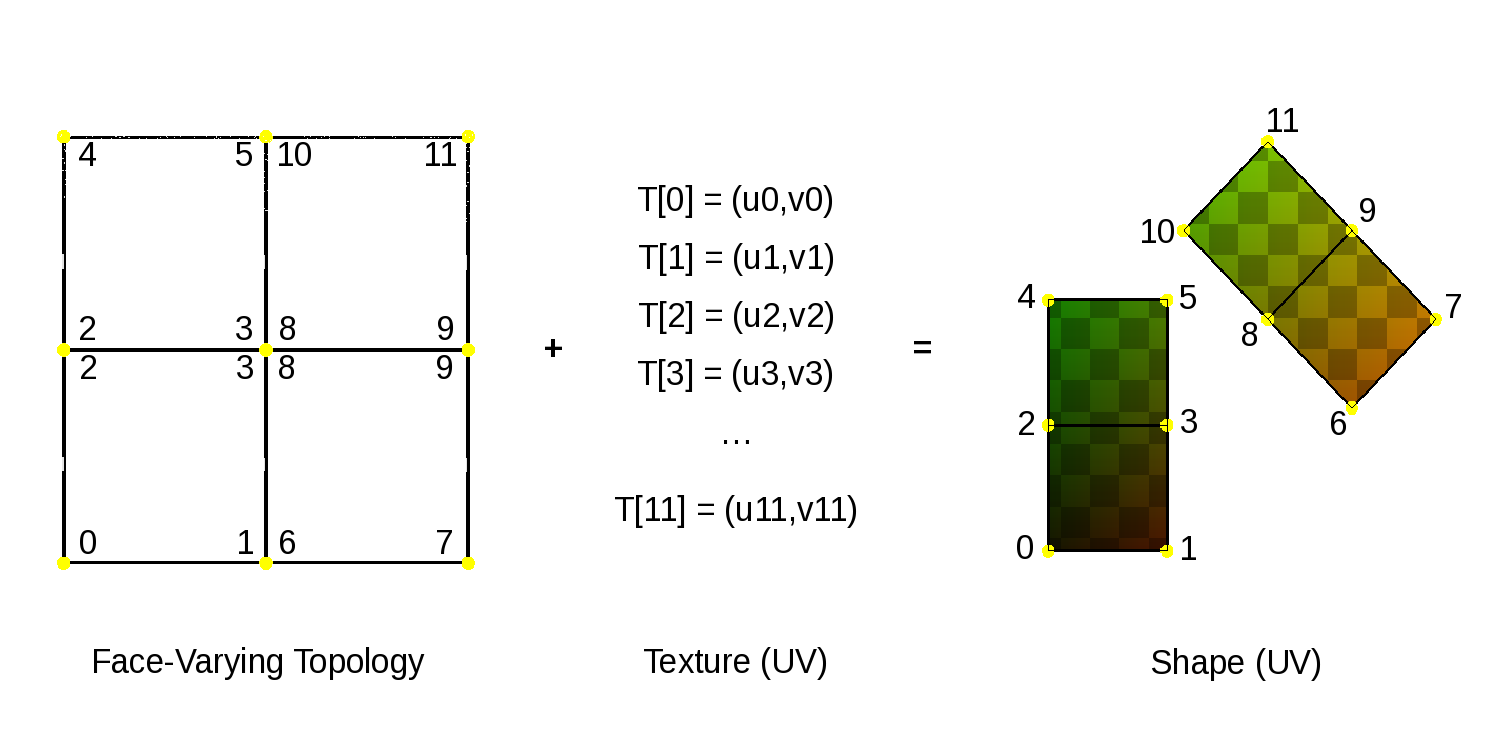
This method of associating data values with the face-vertices of the mesh is said to be assigning "face-varying" data for "face-varying" interpolation. An interpolated value will vary continuously within a face (i.e. the patch of the limit surface associated with the face) but not necessarily across the edges or vertices shared with adjacent faces.
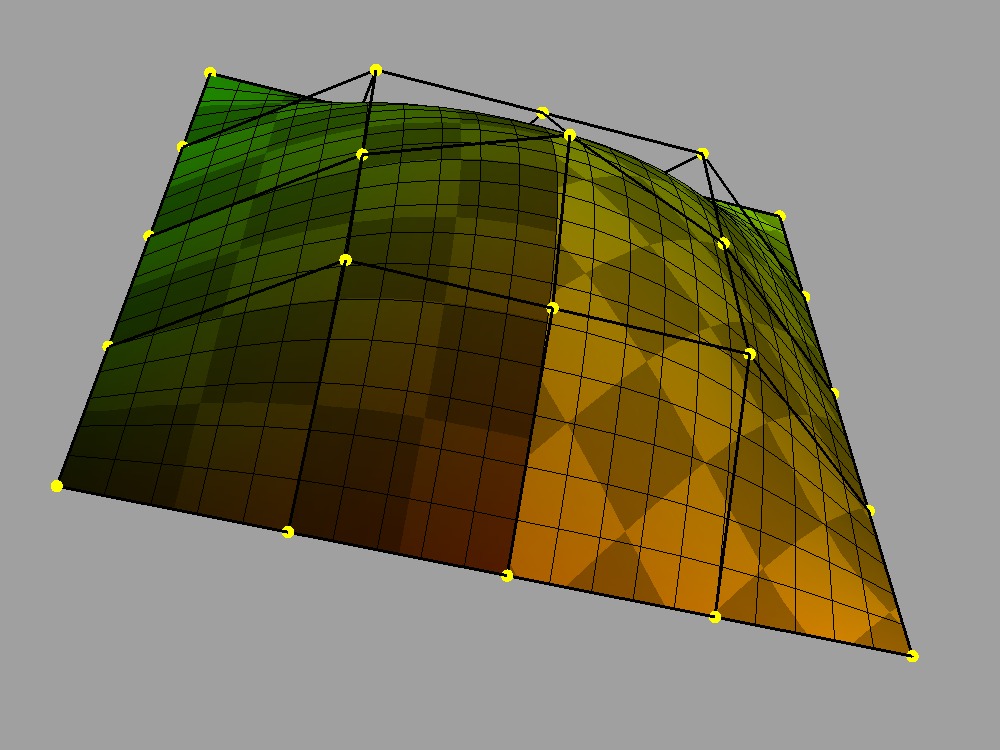
Disjoint face-varying UV regions applied to the limit surface |
The combination of associating data values not with the vertices (the control points) but the face corners, and the resulting data-dependent discontinuities that result, make this a considerably more complicated approach than vertex or varying. The added complexity of the data alone is reason to only use it when necessary, i.e. when discontinuities are desired and present.
Part of the complexity of dealing with face-varying data and interpolation is the way in which the interpolation behavior can be defined. Where the data is continuous, the interpolation can be specified to be as smooth as the underlying limit surface of vertex data or simply linear as achieved with varying data. Where the data is discontinuous -- across interior edges and around vertices -- the discontinuities create boundaries for the data, and partition the underlying surface into disjoint regions. The interpolation along these boundaries can also be specified as smooth or linear in a number of ways (many of which have a historical basis).
A more complete description of the different linear interpolation options with face-varying data and interpolation is given later. These options make it possible to treat the data as either vertex or varying, but with the added presence of discontinuities.
An essential point to remember with face-varying interpolation is that each set of data is free to have its own discontinuities -- this leads to each data set having both unique topology and size.
The topology specified for a collection of face-varying data is referred to as a channel and is unique to face-varying interpolation. Unlike vertex and varying interpolation, which both associate a data value with a vertex, the number of values in a face-varying channel is not fixed by the number of vertices or faces. The number of indices assigned to the face-corners will be the same for all channels, but the number of unique values referred to by these indices may not. We can take advantage of the common mesh topology in areas where the data is continuous, but we lose some of those advantages around the discontinuities. This results in the higher complexity and cost of a face-varying channel compared to vertex or varying data. If the topology for a channel is fixed, though, similar techniques can be applied to factor computation related to the topology so that changes to the data can be processed efficiently.
Schemes and Options
While previous sections have described subdivision surfaces in more general terms, this section describes a number of common variations (often referred to as extensions to the subdivision algorithms) and the ways that they are represented in OpenSubdiv.
The number and nature of the extensions here significantly complicate what are otherwise fairly simple subdivision algorithms. Historically applications have supported either a subset or have had varying implementations of the same feature. OpenSubdiv strives to provide a consistent and efficient implementation of this feature set.
Given the varying presentations of some of these features elsewhere, the naming chosen by OpenSubdiv is emphasized here.
Subdivision Schemes
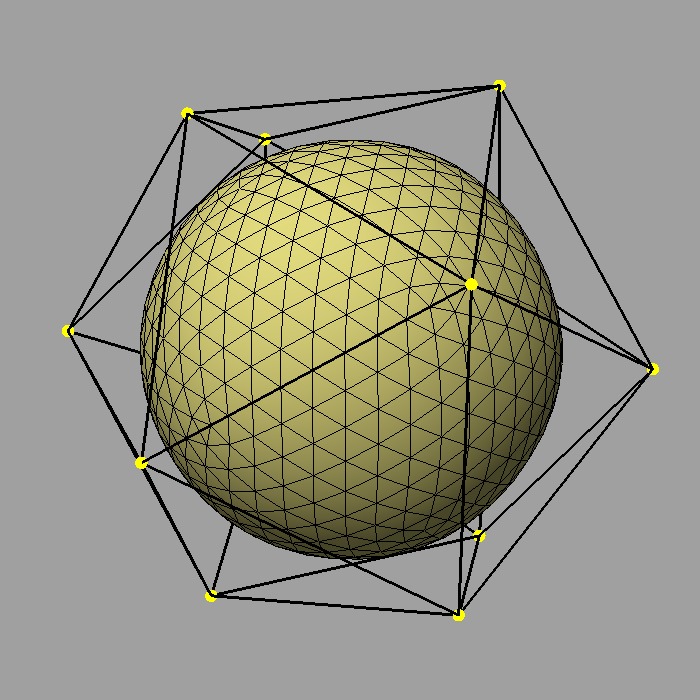
OpenSubdiv provides two well known subdivision surface types -- Catmull-Clark (often referred to more tersely as "Catmark") and Loop subdivision. Catmull-Clark is more widely used and suited to quad-dominant meshes, while Loop is preferred for (and requires) purely triangulated meshes.
The many examples from previous sections have illustrated the more popular Catmull-Clark scheme. For an example of Loop:

|

|

|
|
Boundary Interpolation Rules
Boundary interpolation rules control how subdivision and the limit surface behave for faces adjacent to boundary edges and vertices.
The following choices are available via the enumeration Sdc::Options::VtxBoundaryInterpolation:
| Mode | Behavior |
|---|---|
| VTX_BOUNDARY_NONE | No boundary edge interpolation is applied by default; boundary faces are tagged as holes so that the boundary vertices continue to support the adjacent interior faces, but no surface corresponding to the boundary faces is generated; boundary faces can be selectively interpolated by sharpening all boundary edges incident the vertices of the face |
| VTX_BOUNDARY_EDGE_ONLY | A sequence of boundary vertices defines a smooth curve to which the limit surface along boundary faces extends |
| VTX_BOUNDARY_EDGE_AND_CORNER | Similar to edge-only but the smooth curve resulting on the boundary is made to interpolate corner vertices (vertices with exactly one incident face) |
On a grid example:
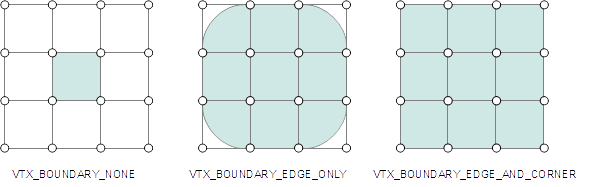
In practice, it is rare to use no boundary interpolation at all -- this feature has its uses in allowing separate meshes to be seamlessly joined together by replicating the vertices along boundaries, but these uses are limited. Given the global nature of the setting, it is usually preferable to explicitly make the boundary faces holes in the areas where surfaces from separate meshes are joined, rather than sharpening edges to interpolate the desired boundaries everywhere else.
The remaining "edge only" and "edge and corner" choices are then solely distinguished by whether or not the surface at corner vertices is smooth or sharp.
Face-varying Interpolation Rules
Face-varying interpolation rules control how face-varying data is interpolated both in the interior of face-varying regions (smooth or linear) and at the boundaries where it is discontinuous (constrained to be linear or "pinned" in a number of ways). Where the topology is continuous and the interpolation chosen to be smooth, the behavior of face-varying interpolation will match that of the vertex interpolation.
Choices for face-varying interpolation are most commonly available in the context of UVs for texture coordinates and a number of names for such choices have evolved in different applications over the years. The choices offered by OpenSubdiv cover a wide range of popular applications. The feature is named face-varying linear interpolation -- rather than boundary interpolation commonly used -- to emphasize that it can be applied to the entire surface (not just boundaries) and that the effects are to make the surface behave more linearly in various ways.
The following choices are available for the Sdc::Options::FVarLinearInterpolation enum -- the ordering here applying progressively more linear constraints:
| Mode | Behavior |
|---|---|
| FVAR_LINEAR_NONE | smooth everywhere the mesh is smooth |
| FVAR_LINEAR_CORNERS_ONLY | linearly interpolate (sharpen or pin) corners only |
| FVAR_LINEAR_CORNERS_PLUS1 | CORNERS_ONLY + sharpening of junctions of 3 or more regions |
| FVAR_LINEAR_CORNERS_PLUS2 | CORNERS_PLUS1 + sharpening of darts and concave corners |
| FVAR_LINEAR_BOUNDARIES | linear interpolation along all boundary edges and corners |
| FVAR_LINEAR_ALL | linear interpolation everywhere (boundaries and interior) |
These rules cannot make the interpolation of the face-varying data smoother than that of the vertices. The presence of sharp features of the mesh created by sharpness values, boundary interpolation rules, or the subdivision scheme itself (e.g. Bilinear) take precedence.
All face-varying interpolation modes illustrated in UV space using a simple 4x4 grid of quads segmented into three UV regions (their control point locations implied by interpolation in the FVAR_LINEAR_ALL case):

(For those familiar, this shape and its assigned UV sets are available for inspection in the "catmark_fvar_bound1" shape of OpenSubdiv's example and regression shapes.)
Semi-Sharp Creases
Just as some types of parametric surfaces support additional shaping controls to affect creasing along the boundaries between surface elements, OpenSubdiv provides additional sharpness values or "weights" associated with edges and vertices to achieve similar results over arbitrary topology.
Setting sharpness values to a maximum value (10 in this case -- a number chosen for historical reasons) effectively modifies the subdivision rules so that the boundaries between the piecewise smooth surfaces are infinitely sharp or discontinuous.
But since real world surfaces never really have infinitely sharp edges, especially when viewed sufficiently close, it is often preferable to set the sharpness lower than this value, making the crease "semi-sharp". A constant weight value assigned to a sequence of edges connected edges therefore enables the creation of features akin to fillets and blends without adding extra rows of vertices (though that technique still has its merits):

Sharpness values range from 0-10, with a value of 0 (or less) having no effect on the surface and a value of 10 (or more) making the feature completely sharp.
It should be noted that infinitely sharp creases are really tangent discontinuities in the surface, implying that the geometric normals are also discontinuous there. Therefore, displacing along the normal will likely tear apart the surface along the crease. If you really want to displace a surface at a crease, it may be better to make the crease semi-sharp.
Other Options
While the preceding options represent features available in a wide-variety of tools and modeling formats, a few others exist whose recognition and adoption is more limited. In some cases, they offer improvements to undesirable behavior of the subdivision algorithms, but their effects are less than ideal.
Given both their limited effectiveness and lack of recognition, these options should be used with caution.
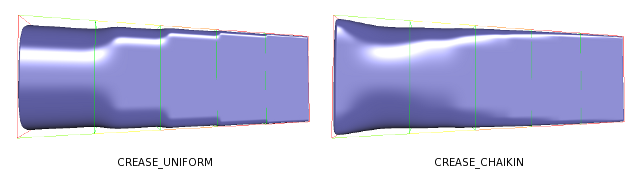
Chaikin Rule
The "Chaikin Rule" is a variation of the semi-sharp creasing method that attempts to improve the appearance of creases along a sequence of connected edges when the sharpness values differ. This choice modifies the subdivision of sharpness values using Chaikin's curve subdivision algorithm to consider all sharpness values of edges around a common vertex when determining the sharpness of child edges.
The creasing method can be set using the values defined in the enumeration Sdc::Options::CreasingMethod:
| Mode | Behavior |
|---|---|
| CREASE_UNIFORM | Apply regular semi-sharp crease rules |
| CREASE_CHAIKIN | Apply "Chaikin" semi-sharp crease rules |
Example of contiguous semi-sharp creases interpolation:
"Triangle Subdivision" Rule
The triangle subdivision rule is a rule added to the Catmull-Clark scheme that modifies the behavior at triangular faces to improve the undesirable surface artefacts that often result in such areas.
| Mode | Behavior |
|---|---|
| TRI_SUB_CATMARK | Default Catmark scheme weights |
| TRI_SUB_SMOOTH | "Smooth triangle" weights |
Cylinder example :

This rule was empirically determined to make triangles subdivide more smoothly. However, this rule breaks the nice property that two separate meshes can be joined seamlessly by overlapping their boundaries; i.e. when there are triangles at either boundary, it is impossible to join the meshes seamlessly
